Rozwiązanie
Krok 1. Ustalenie miejsc zerowych.
Zazwyczaj rozwiązujemy nierówność kwadratową wyznaczając miejsca zerowe, których potem używamy do narysowania wykresu i odczytania rozwiązania. Tym razem mamy zadanie odwrotne, czyli na podstawie rozwiązania nierówności, musimy dojść do miejsc zerowych. Jeżeli rozwiązaniem nierówności jest przedział \((-2, 3)\), to rozwiązując standardową nierówność kwadratową narysowalibyśmy taki oto wykres:
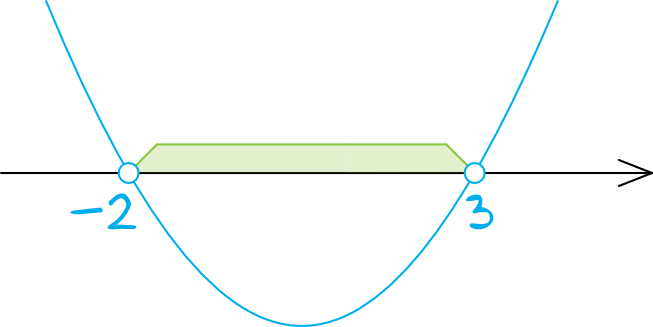
To oznacza, że w trakcie rozwiązywania nierówności powinniśmy otrzymać dwa miejsca zerowe, czyli \(x=-2\) oraz \(x=3\).
Krok 2. Obliczenie wartości \(k\).
Mamy nierówność w postaci iloczynowej. Jak rozwiązujemy taką nierówność? Musimy najpierw poznać jej miejsca zerowe, czyli przyrównać lewą stronę do zera, zatem:
$$(3x-9)(x+k)=0 \\
3x-9=0 \quad\lor\quad x+k=0 \\
3x=9 \quad\lor\quad x=-k \\
x=3 \quad\lor\quad x=-k$$
Z poprzedniego kroku wiemy, że ta nierówność ma dwa miejsca zerowe. Widzimy, że \(x=3\) wychodzi nam z pierwszego nawiasu, więc wniosek z tego płynie taki, że z tego drugiego nawiasu musimy otrzymać to drugie miejsce, czyli \(x=-2\). Skoro tak, to podstawiając \(x=-2\) do równania \(x=-k\), otrzymamy:
$$-2=-k \\
k=2$$