Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Nanosząc na rysunek dane z treści zadania otrzymamy:
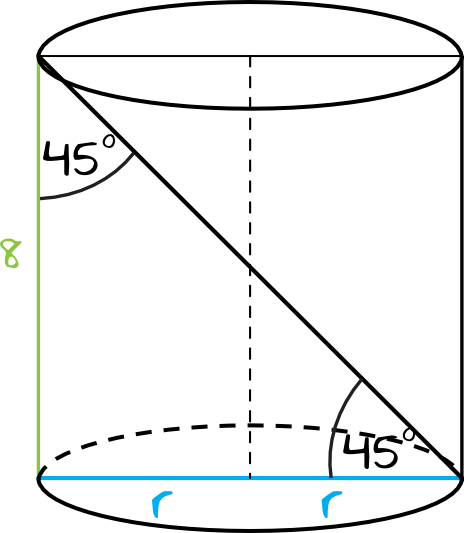
Krok 2. Obliczenie długości promienia podstawy.
Z własności trójkątów o kątach \(45°, 45°, 90°\) wynika, że przyprostokątne mają tą samą długość. Skoro tak, to średnica okręgu znajdującego się w podstawie ma także długość równą \(8\), a to z kolei oznacza, że promień okręgu ma długość:
$$r=8:2=4$$
Krok 3. Obliczenie objętości walca.
Znając długość promienia możemy już bez przeszkód obliczyć objętość całej bryły.
$$V=P_{p}\cdot H \\
V=\pi\cdot r^2\cdot H \\
V=\pi\cdot4^2\cdot8 \\
V=\pi\cdot16\cdot8 \\
V=128\pi$$