Matura z matematyki (poziom podstawowy) - Maj 2013
Zadanie 1. (1pkt) Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność \(|x+4|\lt5\).
Wyjaśnienie:
Musimy poprawnie rozwiązać nierówność z wartością bezwzględną:
$$x+4\lt5 \quad\land\quad x+4\gt-5 \\
x\lt1 \quad\land\quad x\gt-9 \\
x\in(-9;1)$$
Prawidłowy jest więc zbiór przedstawiony w pierwszej odpowiedzi.
Zadanie 26. (2pkt) Rozwiąż równanie \(x^3+2x^2-8x-16=0\).
Odpowiedź
\(x=2\sqrt{2} \quad\lor\quad x=-2\sqrt{2} \quad\lor\quad x=-2\)
Wyjaśnienie:
Krok 1. Wyłączenie odpowiednich czynników przed nawias i zapisanie równania w postaci iloczynowej.
$$x^3+2x^2-8x-16=0 \\
x^2(x+2)-8(x+2)=0 \\
(x^2-8)(x+2)=0$$
Krok 2. Wyznaczenie rozwiązań z postaci iloczynowej.
Aby wartość obliczona w pierwszym kroku była równa zero, to wartość w jednym z nawiasów musi być równa zero. Czyli:
$$x^2-8=0 \quad\lor\quad x+2=0 \\
x=\sqrt{8} \quad\lor\quad x=-\sqrt{8} \quad\lor\quad x=-2$$
Możemy jeszcze wyłączyć czynnik przed znak pierwiastka i zapisać, że rozwiązaniem równania są liczby:
$$x=2\sqrt{2} \quad\lor\quad x=-2\sqrt{2} \quad\lor\quad x=-2$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy pogrupujesz wyrazy i wyłączysz odpowiednie czynniki przed nawias w taki sposób, że w nawiasach jest jednakowa wartość, dzięki której można szybko przejść do postaci iloczynowej albo wręcz doprowadzisz równanie do postaci iloczynowej (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 27. (2pkt) Kąt \(α\) jest ostry i \(sinα=\frac{\sqrt{3}}{2}\). Oblicz wartość wyrażenia \(sin^2α-3cos^2α\).
Odpowiedź
\(sin^2α-3cos^2α=0\)
Wyjaśnienie:
W zadaniu wykorzystamy tzw. "jedynkę trygonometryczną", czyli \(sin^2α+cos^2α=1\).
Krok 1. Obliczenie wartości \(sin^2α\) oraz \(cos^2α\).
$$sin^2α=\left(\frac{\sqrt{3}}{2}\right)^2 \\
sin^2α=\frac{3}{4} \\
\text{oraz} \\
cos^2α=1-sin^2 \\
cos^2α=1-\frac{3}{4} \\
cos^2α=\frac{1}{4}$$
Krok 2. Obliczenie wartości wyrażenia \(sin^2α-3cos^2α\).
$$sin^2α-3cos^2α=\frac{3}{4}-3\cdot\frac{1}{4}=\frac{3}{4}-\frac{3}{4}=0$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
ALBO
• Gdy rozwiązujesz zadanie metodą graficzną (rysując trójkąt prostokątny) i źle zaznaczysz kąt \(α\) lub źle zapiszesz stosunek długości boków w danej funkcji trygonometrycznej.
1 pkt
• Gdy obliczysz wartość \(cos^2α=\frac{1}{4}\) lub \(cosα=\frac{1}{2}\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 28. (2pkt) Udowodnij, że dla dowolnych liczb rzeczywistych \(x,y,z\) takich, że \(x+y+z=0\), prawdziwa jest nierówność \(xy+yz+zx\le0\).
Możesz skorzystać z tożsamości \((x+y+z)^2=x^2+y^2+z^2+2xy+2xz+2yz\).
Odpowiedź
Udowodniono przekształcając wskazaną tożsamość.
Wyjaśnienie:
Krok 1. Przekształcenie tożsamości \((x+y+z)^2=x^2+y^2+z^2+2xy+2xz+2yz\).
W zadaniu skorzystamy z tożsamości podanej w treści zadania. Spróbujemy ją przekształcić w taki sposób, by po lewej stronie otrzymać wartość \(xy+yz+zx\). Zatem:
$$(x+y+z)^2=x^2+y^2+z^2+2xy+2xz+2yz \\
(x+y+z)^2-x^2-y^2-z^2=2xy+2xz+2yz \\
xy+xz+yz=\frac{(x+y+z)^2-x^2-y^2-z^2}{2}$$
Krok 2. Interpretacja otrzymanego równania.
Z treści zadania wiemy, że \(x+y+z=0\), stąd też wartość \((x+y+z)^2\) otrzymana w liczniku jest równa \(0\). Zostaje nam więc tak naprawdę:
$$xy+xz+yz=\frac{-x^2-y^2-z^2}{2}$$
Jakakolwiek liczba podniesiona do kwadratu jest liczbą nieujemną. Skoro więc przed \(x^2\), \(y^2\) oraz \(z^2\) stoją znaki minusa, to na pewno w liczniku mamy wartość niedodatnią, a to z kolei jest dowodem na to, że \(xy+yz+zx\le0\).
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie przekształcisz podane równanie, korzystając z tożsamości podanej w treści zadania (patrz: Krok 1.).
ALBO
• Gdy przekształcisz równanie w taki sposób, że otrzymasz równanie z dwiema niewiadomymi.
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Zadanie 29. (2pkt) Na rysunku przedstawiony jest wykres funkcji \(f(x)\) określonej dla \(x\in\langle-7;8\rangle\).
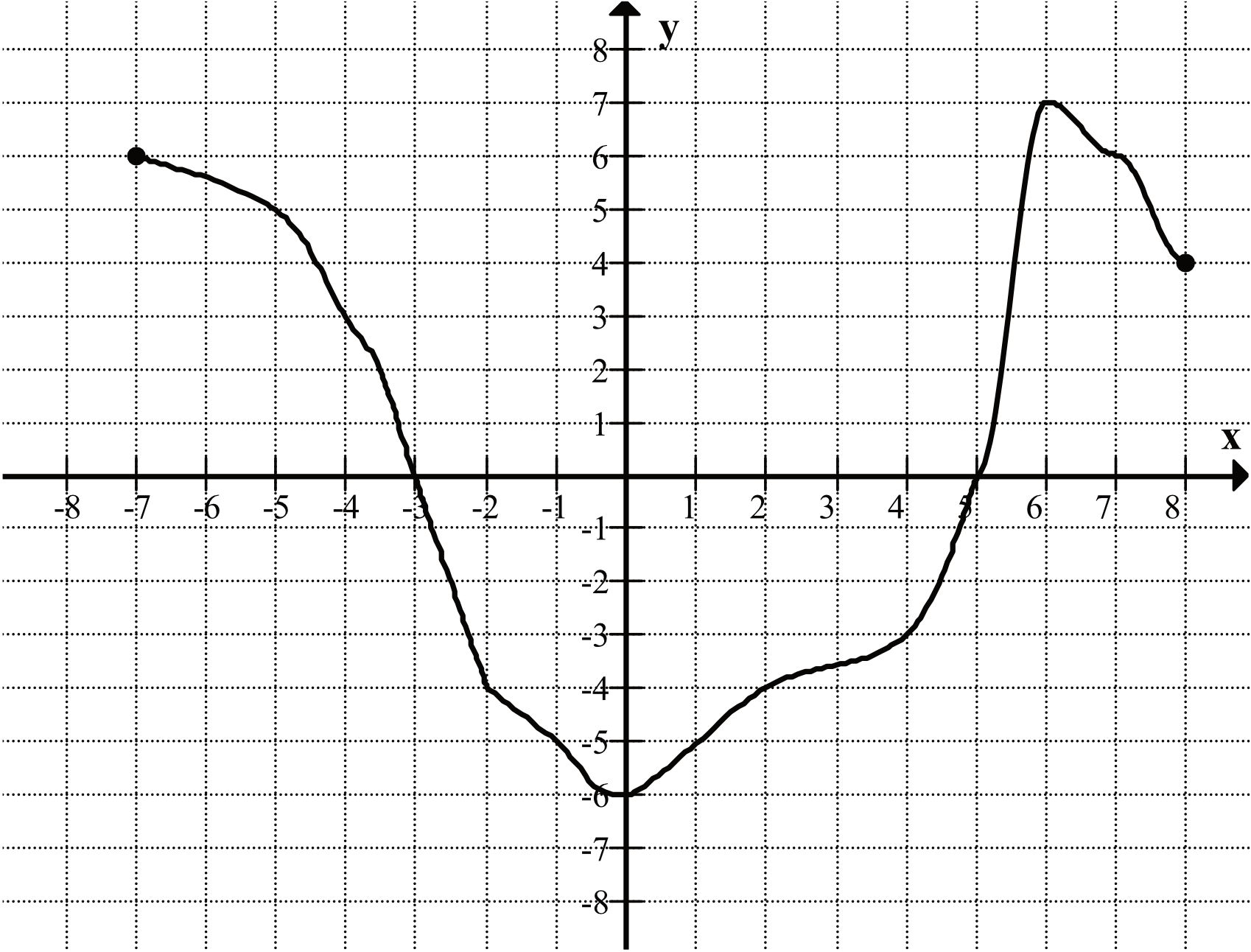
Odczytaj z wykresu i zapisz:
a) największą wartość funkcji \(f\)
b) zbiór rozwiązań nierówności \(f(x)\lt0\)
Odpowiedź
a) Największa wartość funkcji to \(y_{max}=7\).
b) \(x\in(-3;5)\)
Wyjaśnienie:
Krok 1. Odczytanie największej wartości funkcji \(f\).
Najwyżej położonym punktem na wykresie jest ten o współrzędnych \((6;7)\) w związku z tym największą wartością funkcji jest \(7\).
Krok 2. Odczytanie zbioru rozwiązań nierówności \(f(x)\lt0\).
Interesuje nas teraz informacja dla jakich argumentów \(x\) funkcja przyjmuje wartości ujemne, czyli tak naprawdę kiedy funkcja znalazła się pod osią \(Ox\). Szukanym zbiorem rozwiązań jest więc \(x\in(-3;5)\).
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie podasz największą wartość funkcji (patrz: Krok 1.).
ALBO
• Gdy podasz zbiór rozwiązań tej nierówności (patrz: Krok 2.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 30. (2pkt) Rozwiąż nierówność \(2x^2-7x+5\ge0\).
Odpowiedź
\(x\in(-\infty;1\rangle\cup\langle2\frac{1}{2};+\infty)\)
Wyjaśnienie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=2,\;b=-7,\;c=5\)
$$Δ=b^2-4ac=(-7)^2-4\cdot2\cdot5=49-40=9 \\
\sqrt{Δ}=\sqrt{9}=3$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-7)-3}{2\cdot2}=\frac{7-3}{4}=\frac{4}{4}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-7)+3}{2\cdot2}=\frac{7+3}{4}=\frac{10}{4}=2\frac{1}{2}$$
Krok 2. Szkicowanie wykresu paraboli.
Współczynnik \(a=2\), czyli jest dodatni. To oznacza, że parabola musi mieć ramiona skierowane ku górze. Zaznaczamy na osi miejsca zerowe obliczone przed chwilą i szkicujemy wykres paraboli:

Punkty \(x=1\) oraz \(x=2\frac{1}{2}\) mają zamalowane kropki, bo w nierówności wystąpił znak \(\ge\).
Krok 3. Odczytanie rozwiązania.
Interesującym nas przedziałem jest ten, dla którego zbiór argumentów przyjmuje wartość większą lub równą zero. Czyli patrzymy w których miejscach wykres funkcji znalazł się nas osią \(Ox\) lub na niej.
Tym zbiorem jest: \(x\in(-\infty;1\rangle\cup\langle2\frac{1}{2};+\infty)\).
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz miejsca zerowe, a w dalszej części zadania popełnisz błędy (patrz: Krok 1.).
ALBO
• Gdy błędnie wyznaczysz miejsca zerowe funkcji (np. w wyniku błędu rachunkowego przy liczeniu delty), ale dalszy tok rozwiązywania będzie poprawny.
2 pkt
• Gdy otrzymasz oczekiwany wynik (w postaci zapisanego przedziału lub w formie graficznej).
Zadanie 31. (2pkt) Wykaż, że liczba \(6^{100}-2\cdot6^{99}+10\cdot6^{98}\) jest podzielna przez \(17\).
Odpowiedź
Udowodniono wyłączając odpowiednie czynniki przed nawias.
Wyjaśnienie:
Aby móc udowodnić, że wskazana liczba jest podzielna przez \(17\) najlepiej byłoby z całego zapisu wyłączyć liczbę \(17\) (lub jej wielokrotność) i właśnie w ten sposób udowodnimy wskazaną tezę.
Krok 1. Wyłączenie przed nawias wartości \(6^{98}\).
$$6^{100}-2\cdot6^{99}+10\cdot6^{98}= \\
=6^{98}\cdot(6^2-2\cdot6+10)= \\
=6^{98}\cdot(36-12+10)= \\
=6^{98}\cdot34=6^{98}\cdot2\cdot17$$
Krok 2. Interpretacja obliczeń i zakończenie dowodzenia.
Liczbę \(6^{100}-2\cdot6^{99}+10\cdot6^{98}\) przedstawiliśmy w formie mnożenia \(6^{98}\cdot2\cdot17\), którego jeden z czynników jest równy \(17\). To znaczy, że cała liczba jest podzielna przez \(17\), a wynikiem tego dzielenia byłoby \(6^{98}\cdot2\).
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyłączysz odpowiedni czynnik przed nawias np. otrzymując postać \(6^{98}\cdot(6^2-2\cdot6+10)\) lub \(6^{98}\cdot34\) (patrz: Krok 1.) i nie udowodnisz dlaczego ta liczba jest podzielna przez \(17\).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Zadanie 32. (4pkt) Punkt \(S\) jest środkiem okręgu opisanego na trójkącie ostrokątnym \(ABC\). Kąt \(ACS\) jest trzy razy większy od kąta \(BAS\), a kąt \(CBS\) jest dwa razy większy od kąta \(BAS\). Oblicz kąty trójkąta \(ABC\).
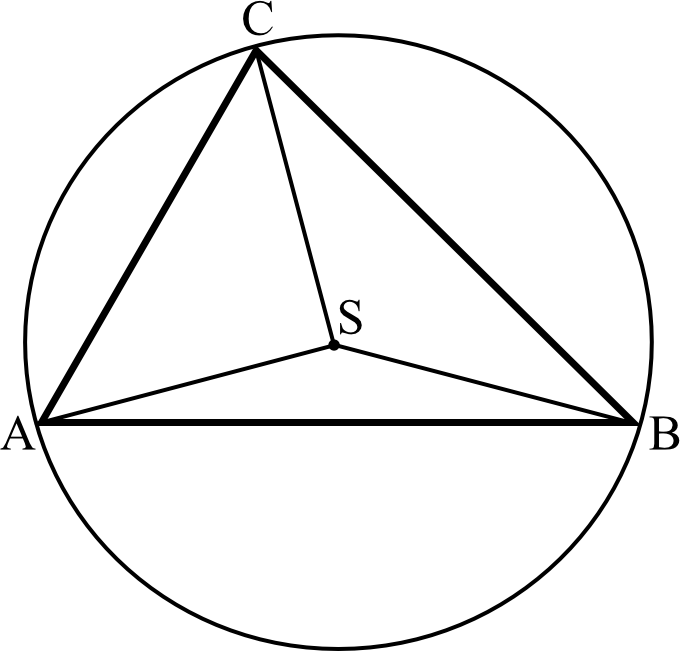
Odpowiedź
\(|\sphericalangle ABC|=45°, |\sphericalangle BCA|=75°, |\sphericalangle CAB|=60°\)
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Musimy dostrzec, że trójkąty \(ABS\), \(BSC\) i \(ASC\) są równoramienne, bo każdy z nich ma dwa ramiona o długości promienia okręgu. Trójkąty równoramienne mają tę cechę, że przy podstawie posiadają dwa kąty identycznej miary. W związku z tym, jeśli oznaczymy sobie jako \(α\) kąt \(BAS\), to także kąt \(ABS\) jest równy \(α\).
Z treści zadania wiemy też, że kąt \(CBS\) jest dwa razy większy od kąta \(BAS\), czyli zgodnie z naszymi oznaczeniami miara kąta \(CBS\) jest równa \(2α\). To oznacza, że i kąt \(BCS\) ma miarę \(2α\). I analogicznie skoro kąt \(ACS\) jest równy \(3α\), to i kąt \(CAS\) ma miarę \(3a\). Oznaczmy sobie wszystkie te dane na rysunku pomocniczym.
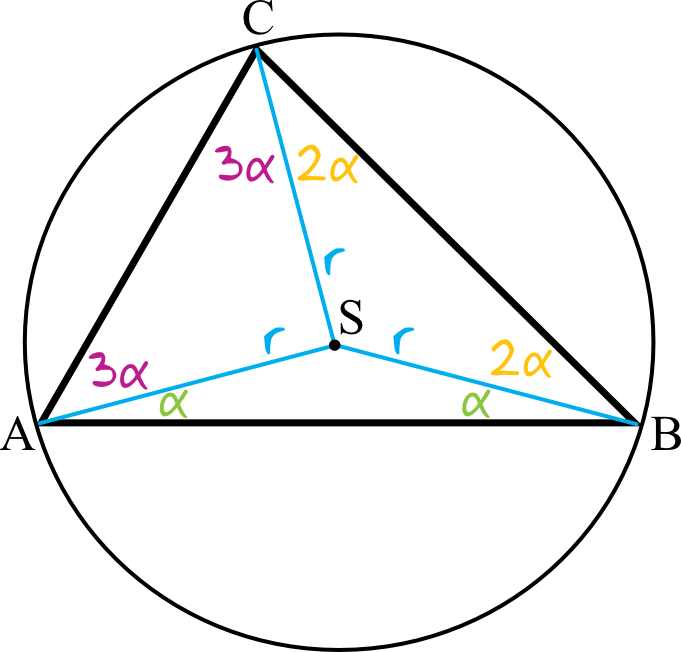
Krok 2. Obliczenie miar kątów trójkąta \(ABC\).
Suma kątów w trójkącie jest równa \(180°\). Na rysunku widzimy, że:
$$|\sphericalangle ABC|+|\sphericalangle BCA|+|\sphericalangle CAB|=3α+5α+4α=12α$$
To oznacza, że bardzo łatwo możemy wyznaczyć wartość \(α\) i tym samym obliczyć miarę każdego z kątów.
$$12α=180° \\
α=15°$$
Zatem:
$$|\sphericalangle ABC|=3α=3\cdot15°=45° \\
|\sphericalangle BCA|=5α=5\cdot15°=75° \\
|\sphericalangle CAB|=4α=4\cdot15°=60°$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz miary kątów \(BAS\), \(ACS\) i \(CBS\) używając jednej zmiennej, np. \(|\sphericalangle BAS|=α\), \(|\sphericalangle ACS|=3α\) i \(|\sphericalangle CBS|=2α\) (patrz: Krok 1.).
2 pkt
• Gdy oprócz zapisania miar kątów \(BAS\), \(ACS\) i \(CBS\) dostrzeżesz, że poszczególne trójkąty są równoramienne i tym samym będą miały one jednakowe miary przy swoich podstawach (patrz: Krok 1.).
ALBO
• Gdy oprócz zapisania miar kątów \(BAS\), \(ACS\) i \(CBS\) wykorzystasz własności kątów środkowych i wpisanych i tym samym zapiszesz odpowiedni układ równań (może to być układ trzech równań), który pozwoli obliczyć miary tych kątów.
3 pkt
• Gdy otrzymasz równanie \(3α+5α+4α=180°\) i/lub obliczysz, że \(α=15°\).
ALBO
• Gdy obliczysz miarę jednego kąta trójkąta np. \(|\sphericalangle CAB|=60°\).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 33. (4pkt) Pole podstawy prawidłowego ostrosłupa czworokątnego jest równe \(100cm^2\), a jego pole powierzchni bocznej jest równe \(260cm^2\). Oblicz objętość tego ostrosłupa.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.

Do obliczenia objętości potrzebujemy miarę wysokości ostrosłupa, czyli odcinka \(SO\). Obliczmy ją z Twierdzenia Pitagorasa, ale zanim to nastąpi to musimy poznać miary odcinków \(OE\) oraz \(SE\).
Krok 1. Obliczenie długości krawędzi podstawy oraz odcinka \(OE\).
Ostrosłup prawidłowy czworokątny ma w swojej podstawie kwadrat. Skoro pole powierzchni jest równe \(100cm^2\), to długość krawędzi podstawy jest równa \(10cm\).
Odcinek \(OE\) jest równy połowie długości podstawy, czyli \(|OE|=5cm\).
Krok 2. Obliczenie długości odcinka \(SE\), czyli wysokości ściany bocznej ostrosłupa.
Pole powierzchni bocznej jest równe \(260cm^2\). Skoro mamy cztery identyczne trójkątne ściany, a każda z nich ma w podstawie trójkąt, to z tego pola powierzchni będziemy w stanie wyznaczyć wysokość każdego takiego trójkąta, czyli nasz odcinek \(SE\).
$$P_{b}=4\cdot\frac{1}{2}ah \\
260cm^2=4\cdot\frac{1}{2}\cdot10cm\cdot h \\
260cm^2=20cm\cdot h \\
h=13cm$$
Mamy już więc kolejną długość \(|SE|=13cm\).
Krok 3. Obliczenie długości odcinka \(SO\), czyli wysokości ostrosłupa.
Skorzystamy tutaj z Twierdzenia Pitagorasa na trójkącie \(SOE\).
$$a^2+b^2=c^2 \\
|OE|^2+|SO|^2=|SE|^2 \\
(5cm)^2+|SO|^2=(13cm)^2 \\
25cm^2+|SO|^2=169cm^2 \\
|SO|^2=144cm^2 \\
|SO|=12cm \quad\lor\quad |SO|=-12cm$$
Wartość ujemną oczywiście odrzucamy, bo wysokość ostrosłupa nie może być ujemna.
Krok 4. Obliczenie objętości bryły.
Znamy pole podstawy, mamy obliczoną wysokość ostrosłupa, więc wystarczy już tylko podstawić dane do wzoru:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot100cm^2\cdot12cm \\
V=400cm^3$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długość krawędzi podstawy (patrz: Krok 1.).
2 pkt
• Gdy obliczysz wysokość ściany bocznej ostrosłupa (patrz: Krok 2.).
ALBO
• Gdy rozwiążesz zadanie błędnie tylko dlatego, że przymiesz iż pole powierzchni bocznej to pole powierzchni tylko jednej ściany bocznej, a nie suma powierzchni wszystkich ścian bocznych.
3 pkt
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 3.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 34. (5pkt) Dwa miasta łączy linia kolejowa o długości \(336\) kilometrów. Pierwszy pociąg przebył tę drogę w czasie o \(40\) minut krótszym niż drugi pociąg. Średnia prędkość pierwszego pociągu na tej trasie była o \(9km/h\) większa od średniej prędkości drugiego pociągu. Oblicz średnią prędkość każdego z tych pociągów na tej trasie.
Odpowiedź
Prędkość pierwszego pociągu to \(72\frac{km}{h}\), a drugiego to \(63\frac{km}{h}\).
Wyjaśnienie:
Krok 1. Wypisanie informacji z treści zadania.
\(t\) - czas jazdy pierwszego pociągu
\(v\) - prędkość jazdy pierwszego pociągu
\(t+\frac{2}{3}h\) - czas jazdy drugiego pociągu (dodajemy \(\frac{2}{3}\), bo \(40\) minut to \(\frac{2}{3}\) godziny. Gdybyśmy zapisali to jako \(t+40min\) to potem nie moglibyśmy się posługiwać jednostkami \(\frac{km}{h}\))
\(v-9\frac{km}{h}\) - prędkość jazdy drugiego pociągu
\(s=336km\) - długość całej trasy
Krok 2. Zapisanie i rozwiązanie odpowiedniego układu równań.
Skorzystamy tutaj ze wzoru na drogę \(s=v\cdot t\). Podstawiając do niego nasze dane wypisane w pierwszym otrzymamy następujący układ równań:
\begin{cases}
vt=336 \\
(v-9)(t+\frac{2}{3})=336
\end{cases}\begin{cases}
t=\frac{336}{v} \\
vt+\frac{2}{3}v-9t-6=336
\end{cases}
Po podstawieniu wartości \(t\) z pierwszego równania do drugiego otrzymamy:
$$\require{cancel}
v\cdot\frac{336}{v}+\frac{2}{3}v-9\cdot\frac{336}{v}-6=336 \\
\cancel{336}+\frac{2}{3}v-\frac{3024}{v}-6=\cancel{336} \\
\frac{2}{3}v-\frac{3024}{v}-6=0 \quad\bigg/\cdot\frac{3}{2} \\
v-\frac{4536}{v}-9=0 \quad\bigg/\cdot v \\
v^2-9v-4536=0$$
Krok 3. Rozwiązanie powstałego równania kwadratowego.
Współczynniki: \(a=1,\;b=-9,\;c=-4536\)
$$Δ=b^2-4ac=(-9)^2-4\cdot1\cdot(-4536)=81+18144=18225 \\
\sqrt{Δ}=\sqrt{18225}=135$$
$$v_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-9)-135}{2\cdot1}=\frac{9-135}{2}=\frac{-126}{2}=-63 \\
v_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-9)+135}{2\cdot1}=\frac{9+135}{2}=\frac{144}{2}=72$$
Rozwiązanie ujemne wykluczamy, bo prędkość musi być dodatnia. To oznacza, że ostatecznym rozwiązaniem jest \(v=72\frac{km}{h}\).
Krok 4. Obliczenie prędkości drugiego pociągu.
Prędkość jazdy drugiego pociągu to:
$$v-9\frac{km}{h}=72\frac{km}{h}-9\frac{km}{h}=63\frac{km}{h}$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy nie wykonasz jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wprowadzisz sensowne oznaczenia i zapiszesz podstawowe relacje między nimi (patrz: Krok 1.).
2 pkt
• Gdy zapiszesz odpowiednie relacje w formie równania z dwoma niewiadomymi lub w postaci układu równań (patrz: Krok 2.).
3 pkt
• Gdy sprowadzisz obliczenia do postaci równania z jedną niewiadomą, czyli postaci w której występuje jedynie niewiadoma \(v\) lub \(t\) (patrz: Krok 2.).
4 pkt
• Gdy doprowadzisz równanie do postaci ogólnej równania kwadratowego (patrz: Krok 2.), ale samo równanie kwadratowe (patrz: Krok 3.) rozwiążesz błędnie.
ALBO
• Gdy doprowadzisz zadanie do samego końca, ale otrzymany wynik będzie zły jedynie ze względu na błąd rachunkowy.
ALBO
• Gdy źle zinterpretujesz otrzymane wyniki z równania kwadratowego.
5 pkt
• Gdy otrzymasz oczekiwany wynik.


Zadanie 33.skąd wzięła się ta 1/2 ah w tym wzorze na Pb ?
To ze wzoru na pole trójkąta :) Ściany boczne są trójkątami, a skoro mamy cztery takie trójkąty, to Pb jest równe czterem polom trójkąta :)
Nie rozumiem, dlaczego w zadaniu 11 jest odpowiedź C. Wiadomo, że zmiana będzie dotyczyć wartości argumentu x, ale podstawiając dane z wykresu z odpowiedzi C np. f(-7) y=f(-7-2)=f(-9), a na rysunku drugim pierwszą liczbą znajdującą się we fragmencie funkcji jest -5. Nie powinna być w takim razie odpowiedź A y=f(x+2)?
To jest klasyczny problem z przesunięciami w lewo i prawo, są one nieintuicyjne ;) Bardzo dobrze omawiam to na filmikach z kursu, ale i tutaj przypomnę, że jak mamy przesunięcie w prawo, to tam w nawiasie musi być minus (a nie plus jak się często wydaje) i analogicznie jak jest przesunięcie w lewo, to tam w nawiasie byłby plus.
To co rozpisujesz, jest niepoprawne. To trzeba byłoby zapisać, że f(-7) to jest to samo, co po prawej stronie f(-5-2) i teraz zauważ, że lewa funkcja dla x=-7 przyjmuje tą samą wartość co prawa dla x=-5.