W układzie współrzędnych na płaszczyźnie punkty \(A=(2,5)\) i \(C=(6,7)\) są przeciwległymi wierzchołkami kwadratu \(ABCD\). Wyznacz równanie prostej \(BD\).
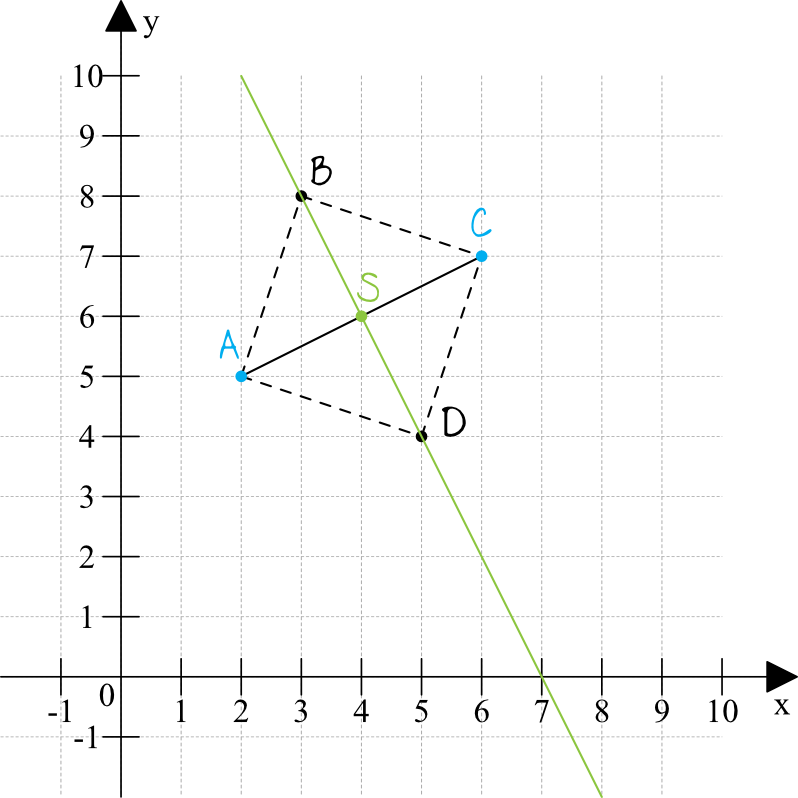
Na początku dobrze jest zaznaczyć sobie w układzie współrzędnych punkty \(A\) oraz \(C\), a także prostą na której znajdą się brakujące punkty \(B\) oraz \(D\). I tu pierwsze bardzo ważne spostrzeżenie – przekątne kwadratu przecinają się dokładnie w połowie swojej długości, a więc nasza prosta będzie na pewno przechodzić przez punkt \(S\), który jest środkiem odcinka \(AC\).
Skorzystamy ze wzorów, które dostępne są w tablicach matematycznych:
$$x_{S}=\frac{x_{A}+x_{C}}{2}=\frac{2+6}{2}=\frac{8}{2}=4 \\
y_{S}=\frac{y_{A}+y_{C}}{2}=\frac{5+7}{2}=\frac{12}{2}=6 \\
S=(4;6)$$
Nasz plan działania jest dość prosty. Wyznaczymy sobie wzór prostej \(AC\), a następnie wzór prostej prostopadłej, która będzie przechodzić przez punkt \(S\). To właśnie ta prosta prostopadła jest przez nas poszukiwana. Prosta \(AC\) przyjmuje postać \(y=ax+b\), więc możemy podstawić pod ten wzór najpierw współrzędne punktu \(A\), następnie punktu \(C\) i w ten sposób stworzymy prosty układ równań:
\begin{cases}
5=2a+b \\
7=6a+b
\end{cases}
Możemy zastosować tu metodę podstawiania, przyjmując z pierwszego równania \(b=5-2a\), jednak znacznie prościej i szybciej będzie po prostu odjąć to równanie stronami. Otrzymamy wtedy:
$$-2=-4a \quad\bigg/:(-4) \\
a=\frac{1}{2}$$
Możemy jeszcze wyznaczyć współczynnik \(b\) tej prostej, choć nie będzie nam on już potrzebny do dalszych obliczeń. Podstawiamy obliczoną przed chwilą wartość współczynnika \(a\) do wybranego równania, otrzymując:
$$5=2\cdot\frac{1}{2}+b \\
5=1+b \\
b=4$$
Wzór prostej przechodzącej przez punkty \(A\) i \(C\) to \(y=\frac{1}{2}+4\).
Prosta \(BD\) będzie na pewno prostopadła do prostej \(AC\) oraz będzie przechodzić przez punkt \(S\). Aby dwie proste były względem siebie prostopadłe to iloczyn ich współczynników kierunkowych \(a\) musi być równy \(-1\). Skoro pierwsza prosta ma współczynnik kierunkowy równy \(\frac{1}{2}\) to druga musi mieć:
$$a\cdot\frac{1}{2}=-1 \\
a=-2$$
Wiemy już, że prosta \(BD\) przyjmuje postać \(y=-2x+b\). Brakuje nam jeszcze tylko współczynnika \(b\). Wyznaczymy go podstawiając współrzędne punktu \(S\), przez który musi ta prosta przechodzić, stąd też:
$$6=-2\cdot4+b \\
6=-8+b \\
b=14$$
Wzór prostej \(BD\) to w takim razie \(y=-2x+14\).
\(y=-2x+14\)

