Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\). Ponadto wiadomo, że \(A=(-2,4)\) i \(B=(6,-2)\). Wierzchołek \(C\) należy do osi \(Oy\). Oblicz współrzędne wierzchołka \(C\).
W treści zadania mamy podane bardzo dokładne współrzędne punktów \(A\) i \(B\), które w dodatku są liczbami całkowitymi, więc możemy wykonać dość przyzwoity rysunek pomocniczy, który przy okazji posłuży nam później do weryfikacji obliczeń. Zastanówmy się też gdzie może znaleźć się nasz punkt \(C\). Na pewno będzie on na osią \(Oy\), ale gdzie tak mniej więcej powinniśmy się go spodziewać? Nad osią iksów, czy pod nią? Na pewno nie może być nad osią, bo nad osią będzie bardzo daleko od punktu \(B\), a jednocześnie blisko punktu \(A\). To nas nie satysfakcjonuje, bo wiemy z relacji \(|AC|=|BC|\), że odległość punktu \(C\) od punktu \(A\) oraz \(B\) jest jednakowa. Ten nasz poszukiwany punkt znajdzie się tuż pod osią iksów – a gdzie dokładnie, to sobie to zaraz obliczymy.
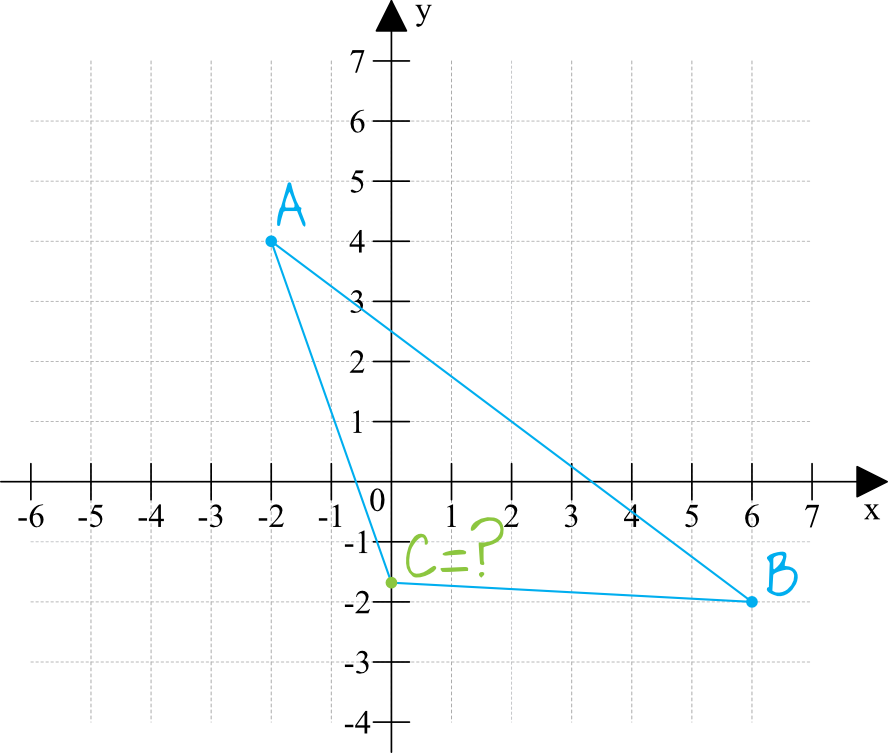
Skorzystamy ze wzorów na długość odcinków w układzie współrzędnych. Znamy współrzędne \(A\) i \(B\), ale to nie wszystko, bo znamy też jeszcze jedną bardzo ważną współrzędną – wiemy, że współrzędna \(x\) punktu \(C\) jest równa \(x_{C}=0\), bo wierzchołek \(C\) leży do osi \(Oy\).
Wiemy też, że \(|AC|=|BC|\), a to z kolei pozwoli nam ułożyć odpowiednie równanie, z którego wyznaczymy sobie brakującą współrzędną \(y_{C}\).
$$\require{cancel}
|AC|=|BC| \\
\sqrt{(x_{C}-x_{A})^2+(y_{C}-y_{A})^2}=\sqrt{(x_{C}-x_{B})^2+(y_{C}-y_{B})^2} \\
(x_{C}-x_{A})^2+(y_{C}-y_{A})^2=(x_{C}-x_{B})^2+(y_{C}-y_{B})^2 \\
(0-(-2))^2+(y_{C}-4)^2=(0-6)^2+(y_{C}-(-2))^2 \\
2^2+(y_{C}-4)^2=(-6)^2+(y_{C}+2)^2 \\
\cancel{4}+\cancel{y_{C}^2}-8y_{c}+16=36+\cancel{y_{C}^2}+4y_{C}+\cancel{4} \\
-12y=20 \\
y_{C}=-\frac{20}{12} \\
y_{C}=-\frac{5}{3}$$
To oznacza, że \(C=\left(0;-\frac{5}{3}\right)\).
\(C=\left(0;-\frac{5}{3}\right)\)

