Funkcja wykładnicza charakteryzuje się tym, że argument \(x\) pojawia się w wykładniku potęgi. Spójrzmy zatem na przykładowe wzory oraz wykresy, omawiając przy tym kluczowe własności funkcji wykładniczej.
Wzór funkcji wykładniczej
$$f(x)=a^x \\
\text{gdzie } a\gt0$$
Przykładowymi funkcjami będą więc np.:
$$f(x)=3^x \\
f(x)=\left(\frac{1}{2}\right)^x \\
f(x)=5^{2x}$$
Zwróć szczególną uwagę, że w zapisie wzoru liczba \(a\) musi być większa od zera. Argument \(x\) może być natomiast dowolną liczbą rzeczywistą.
Wykres funkcji wykładniczej
Kształt wykresu funkcji wykładniczej typu \(y=a^x\) jest uzależniony od podstawy potęgi, czyli od \(a\). Funkcja może być:
· rosnąca dla \(a\gt1\)
· malejąca dla \(0\lt a\lt1\)
· stała dla \(a=1\)
Spójrzmy na przykładowe wykresy funkcji wykładniczych:
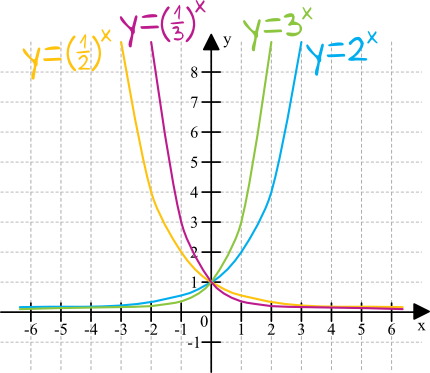
Bazując na powyższych wykresach, możemy zapisać kilka podstawowych własności funkcji wykładniczych:
· dziedziną funkcji wykładniczej jest zbiór liczb rzeczywistych
· zbiorem wartości funkcji wykładniczej jest przedział \((0;+\infty)\)
· asymptotą poziomą wykresu funkcji jest oś \(Ox\)
· wykres przechodzi przez punkt o współrzędnych \((0;1)\)
Szczególną uwagę warto zwrócić zwłaszcza na dwie ostatnie własności. Asymptota to linia, do której wykres się zbliża, ale nigdy jej nie przekracza i tutaj taką linią jest oś \(Ox\). Wykres funkcji nie przetnie więc osi \(Ox\), a to oznacza, że np. nie mamy tutaj miejsc zerowych. Przecinać za to będziemy oś \(Oy\) i tu też bardzo ciekawa obserwacja – niezależnie od wybranej funkcji zawsze dzieje się to w punkcie o współrzędnych \((0;1)\). Wynika to z tego, o czym mówiliśmy sobie w temacie potęg – każda liczba różna od zera podniesiona do potęgi zerowej daje wynik równy \(1\), stąd też niezależnie od wzoru, zawsze dla argumentu \(x=0\) otrzymamy wartość \(y=1\).
Oczywiście funkcja wykładnicza, tak jak każda inna, może być przekształcona/przesunięta, co z kolei sprawi, że zmienią się jej powyższe własności. Przykładowo, funkcja \(f(x)=2^x\) jest standardową funkcją wykładniczą i wszystkie powyższe własności będą jak najbardziej spełnione. Jeżeli jednak przesuniemy tę funkcję o trzy jednostki w górę otrzymując funkcję \(g(x)=2^{x}+3\), to nowa funkcja będzie miała zmieniony zbiór wartości.
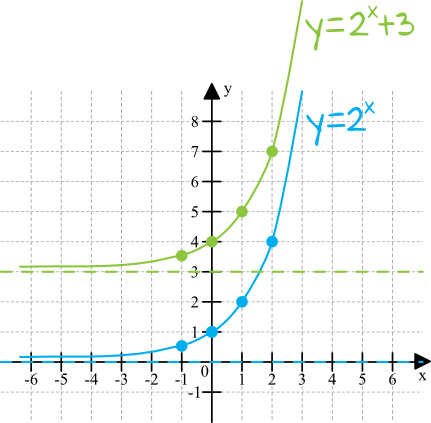
Więcej o przekształceniach wykresów funkcji przeczytasz tutaj:
Spójrzmy teraz na przykładowe zadania z jakimi będziemy mierzyć się w tym temacie.
A. \(f(x)=1^x\)
B. \(f(x)=\left(\frac{1}{5}\right)^x\)
C. \(f(x)=(\sqrt{2})^x\)
D. \(f(x)=(0,04)^x\)
Rozwiązanie:
Funkcja wykładnicza \(f(x)=a^x\) jest rosnąca tylko wtedy, gdy \(a\gt1\). Patrząc się na wzory podanych funkcji widzimy, że ten warunek spełnia jedynie funkcja \(f(x)=(\sqrt{2})^x\), ponieważ \(\sqrt{2}\gt1\), zatem to właśnie będzie funkcja rosnąca.
Rozwiązanie:
Aby poznać wartość \(a\), wystarczy podstawić współrzędne podanego punktu do postaci \(f(x)=a^x\). Czyli w miejsce \(x\) podstawiamy \(2\), a w miejsce \(f(x)\) wpisujemy \(9\), otrzymując:
$$9=a^2$$
Chcąc rozwiązać to równanie musimy sprowadzić lewą i prawą stronę do jednakowego wykładnika potęgi. Wiedząc, że \(9\) jest równe \(3^2\), moglibyśmy zapisać, że:
$$3^2=a^2 \\
a=3$$
Rozwiązanie:
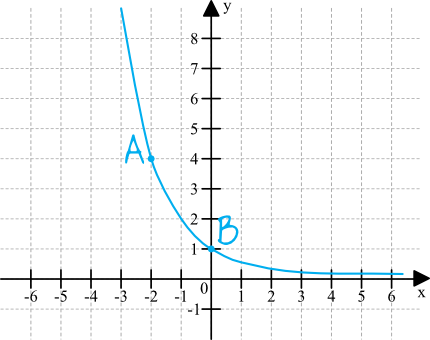
Sytuacja jest niemalże identyczna jak przed chwilą. Różnica jest tylko taka, że tym razem musimy samodzielnie odczytać współrzędne punktu przez które przechodzi wykres tej funkcji. Co ważne, zawsze przy tego typu zadaniach zwracamy uwagę na punkt inny niż ten o współrzędnych \((0;1)\), ponieważ jak już ustaliliśmy, przez ten punkt przechodzą wszystkie wykresy funkcji wykładniczych.
Widzimy, że wykres przechodzi przez punkt \(A\) o współrzędnych \((-2;4)\), czyli podstawiając te współrzędne do postaci \(y=a^x\), powstanie nam do rozwiązania takie oto równanie:
$$4=a^{-2}$$
I tu jest najtrudniejszy moment – musimy sprowadzić lewą i prawą stronę równania do tego samego wykładnika potęgi. Tu z działu potęg powinniśmy pamiętać, że ujemna potęga związana jest z odwrotnością liczby potęgowanej i że w takim razie \(4=2^2=\left(\frac{1}{2}\right)^{-2}\). Moglibyśmy więc zapisać, że:
$$\left(\frac{1}{2}\right)^{-2}=a^{-2} \\
a=\frac{1}{2}$$
Przy okazji możemy zweryfikować poprawność naszych obliczeń. Widzimy, że funkcja jest malejąca, czyli spodziewamy się, że \(a\) jest większe od \(0\) i mniejsze od \(1\). Otrzymany wynik \(a=\frac{1}{2}\) spełnia te warunki, więc wszystko jest w porządku.
Zobacz też:

Hej, chodzi mi o to zdanie- Widzimy, że wykres przechodzi przez punkt o współrzędnych (−2;4). Dlaczego od -2 do 4? jak odczytać odkąd dokąd przechodzi wykres?
Ale to nie jest od -2 do 4, tylko to jest po prostu punkt A=(-2;4) :) Czyli na osi OX szukamy argumentu x=-2 i zerkamy jaką wartość przyjmuje funkcja dla tego argumentu, no i widzimy, że to będzie wartość równa 4 :)