Tworząca stożka o promieniu podstawy 3 ma długość 6

Tworząca stożka o promieniu podstawy \(3\) ma długość \(6\) (zobacz rysunek).

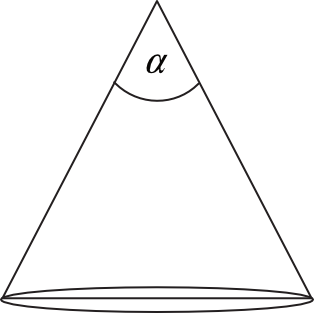
Kąt \(α\) rozwarcia tego stożka jest równy:

Musimy zauważyć, że w przekroju stożka znalazł się trójkąt równoboczny. Skąd to wiemy? Skoro promień stożka jest równy \(3\), to średnica (czyli de facto podstawa trójkąta) ma długość \(6\). Tworząca stożka (czyli ramiona trójkąta) ma także długość \(6\), a to oznacza, że wszystkie boki są jednakowej długości. Dostrzeżenie tej zależności pozwala nam powiedzieć, że kąt \(α=60°\), bowiem w trójkącie równobocznym wszystkie kąty mają miarę \(60°\).

C. \(60°\)