Funkcja logarytmiczna charakteryzuje się tym, że argument \(x\) jest liczbą logarytmowaną. Spójrzmy zatem na przykładowe wzory oraz wykresy, omawiając przy tym kluczowe własności funkcji logarytmicznej.
Wzór funkcji logarytmicznej
$$f(x)=log_{a}x \\
\text{gdzie } a\gt0 \text { oraz } a\neq1$$
Przykładowymi funkcjami będą więc np.:
$$f(x)=log_{3}x \\
f(x)=log_{\frac{1}{2}}x \\
f(x)=log_{2}(x-4)$$
Zwróć uwagę, że liczba \(a\) musi być większa od zera i nie może być równa \(1\). Dodatkowo argument \(x\) zawsze jest liczbą większą od zera (bo nie mamy logarytmów z liczb ujemnych).
Wykres funkcji logarytmicznej
Kształt wykresu funkcji logarytmicznej typu \(y=log_{a}x\) jest uzależniony od podstawy logarytmu, czyli od \(a\). Funkcja może być:
· rosnąca dla \(a\gt1\)
· malejąca dla \(0\lt a\lt1\)
Spójrzmy na przykładowe wykresy funkcji logarytmicznych:
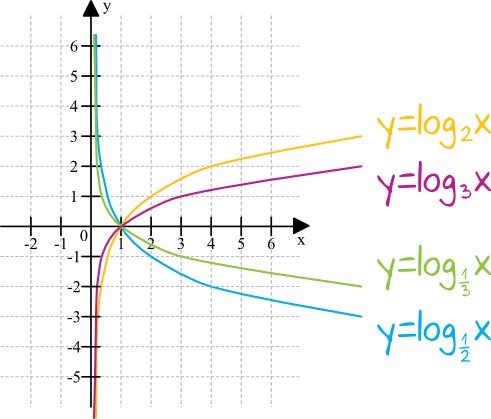
Bazując na powyższych wykresach, możemy zapisać kilka podstawowych własności funkcji logarytmicznych:
· dziedziną funkcji logarytmicznej jest przedział \((0;+\infty)\)
· zbiorem wartości funkcji logarytmicznej jest zbiór liczb rzeczywistych
· asymptotą poziomą wykresu funkcji jest oś \(Oy\)
· wykres przechodzi przez punkt o współrzędnych \(P=(1;0)\)
Szczególną uwagę warto zwrócić zwłaszcza na dwie ostatnie własności. Asymptota to linia, do której wykres się zbliża, ale nigdy jej nie przekracza i tutaj taką linią jest oś \(Oy\). Wykres funkcji nie przetnie więc osi \(Oy\). Przecinać za to będziemy oś \(Ox\) i tu też bardzo ciekawa obserwacja – niezależnie od wybranej funkcji zawsze dzieje się to w punkcie o współrzędnych \((1;0)\). Wynika to z tego, o czym mówiliśmy sobie w temacie logarytmów – jeśli liczba logarytmowana jest równa \(1\), to wynik tego logarytmu jest równy \(0\), stąd też niezależnie od wzoru, zawsze dla argumentu \(x=1\) otrzymamy wartość \(y=0\).
Oczywiście funkcja logarytmiczna, tak jak każda inna, może być przekształcona/przesunięta, co może wpłynąć na jej własności opisane powyżej. Przykładowo, funkcja \(f(x)=log_{3}x\) jest standardową funkcją wykładniczą i wszystkie powyższe własności będą jak najbardziej spełnione. Jeżeli jednak przesuniemy tę funkcję o dwie jednostki w górę otrzymując funkcję \(g(x)=log_{3}x+2\), to nowa funkcja nie będzie już przechodzić przez punkt o współrzędnych \((1;0)\), tylko przejdzie przez punkt \((1;2)\).
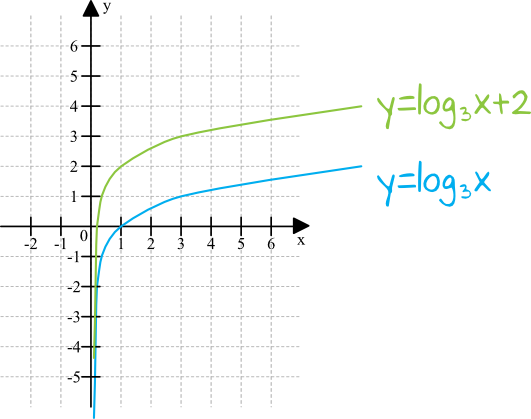
Więcej o przekształceniach wykresów funkcji przeczytasz tutaj:
Spójrzmy teraz na przykładowe zadania z jakimi będziemy mierzyć się w tym temacie.
A. \(f(x)=log_{\frac{1}{3}}x\)
B. \(f(x)=log_{\sqrt{3}}x\)
C. \(f(x)=log_{3}x\)
D. \(f(x)=log_{3}x-3\)
Rozwiązanie:
Funkcja logarytmiczna \(f(x)=log_{a}x\) jest malejąca tylko wtedy, gdy \(a\) jest większe od \(0\) i mniejsze od \(1\). Patrząc się na wzory podanych funkcji widzimy, że ten warunek spełnia jedynie funkcja \(f(x)=log_{\frac{1}{3}}x\), ponieważ \(0\gt\frac{1}{3}\gt1\), zatem to właśnie będzie funkcja malejąca.
Przy okazji – ostatnia funkcja to nic innego jak funkcja \(f(x)=log_{3}x\), która jest przesunięta o \(3\) jednostki w dół. Przesunięcie w dół nie zmienia oczywiście tego, że jest to funkcja rosnąca.
A. \(f(x)=log_{\frac{1}{2}}x\)
B. \(f(x)=log_{\sqrt{2}}x\)
C. \(f(x)=log_{2}x\)
D. \(f(x)=log_{8}x\)
Rozwiązanie:
Do tego zadania można podejść na różne sposoby. Możemy oczywiście podstawić do każdej z odpowiedzi \(x=8\) i sprawdzić, kiedy wartość funkcji będzie równa \(3\), bo taka jest współrzędna \(y\) naszego punktu. Jednak ciekawszą metodą będzie samodzielne sprawdzenie, dla jakiego \(a\) funkcja typu \(f(x)=log_{a}x\) przechodzi przez punkt \((8;3)\). W tym celu moglibyśmy podstawić współrzędne naszego punktu i zapisać, że:
$$3=log_{a}8$$
Z własności logarytmów wiemy, że \(log_{a}8=3\) tylko wtedy, gdy \(a^3=8\). Skoro tak, to sprowadzając lewą i prawą stronę równania do jednakowego wykładnika potęgi, otrzymamy:
$$a^3=8 \\
a^3=2^3 \\
a=2$$
To oznacza, że poszukiwaną funkcją będzie ta, która ma \(a=2\), czyli \(f(x)=log_{2}x\).
Zobacz też:
