Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Nanieśmy na układ współrzędnych poszczególne punkty z treści zadania:
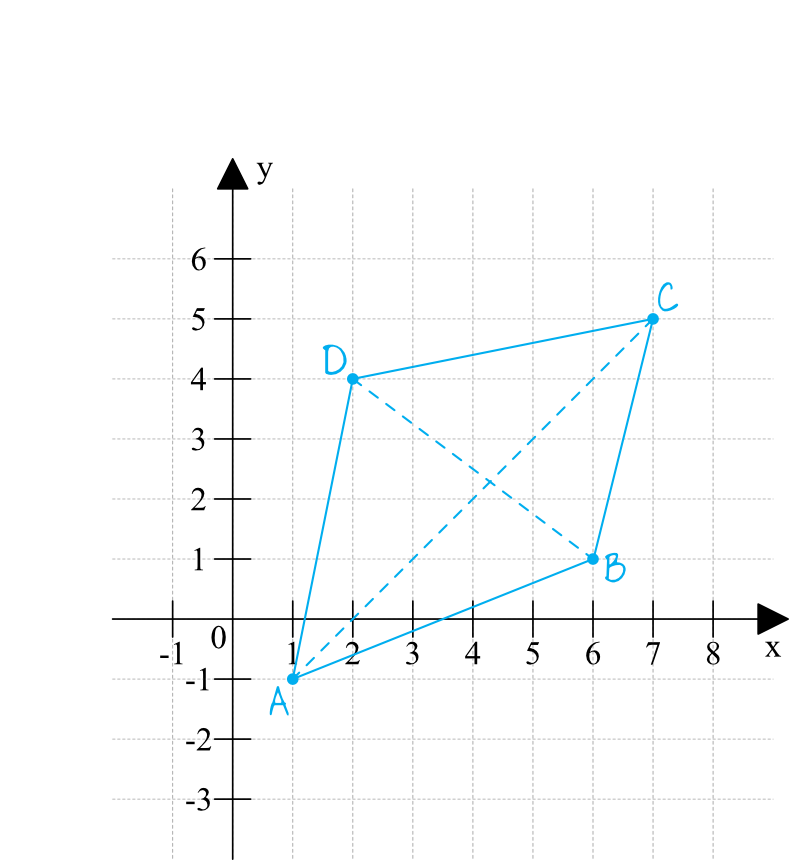
Krok 2. Wyznaczenie równania prostej \(AC\).
Znając współrzędne dwóch punktów możemy bez problemu wyznaczyć równanie prostej, która przez te punkty przechodzi. W tym celu możemy skorzystać z długiego i skomplikowanego wzoru z tablic lub też z metody układu równań - i to właśnie z tego drugiego sposobu skorzystamy.
W tym celu musimy podstawić do równania prostej \(y=ax+b\) najpierw współrzędne punktu \(A\), a następnie punktu \(C\), zatem:
\begin{cases}
-1=a\cdot1+b \\
5=a\cdot7+b
\end{cases}
\begin{cases}
-1=a+b \\
5=7a+b
\end{cases}
Odejmując te równania stronami, otrzymamy:
$$-6=-6a \\
a=1$$
Wartość brakującego współczynnika \(b\) wyznaczymy podstawiając \(a=1\) do wybranego równania z układu równań (np. z pierwszego), zatem:
$$-1=a+b \\
-1=1+b \\
b=-2$$
To oznacza, że prosta \(AC\) wyraża się równaniem \(y=1x-2\), czyli po prostu \(y=x-2\).
Krok 3. Wyznaczenie równania prostej \(BD\).
Równanie prostej \(BD\) wyznaczymy identycznie jak prostej \(AC\), zatem:
\begin{cases}
1=a\cdot6+b \\
4=a\cdot2+b
\end{cases}
\begin{cases}
1=6a+b \\
4=2a+b
\end{cases}
Odejmując te równania stronami, otrzymamy:
$$-3=4a \\
a=-\frac{3}{4}$$
Brakujący współczynnik \(b\) wyznaczymy podstawiając teraz \(a=-\frac{3}{4}\) do wybranego równania z układu równań (np. do pierwszego), zatem:
$$1=6a+b \\
1=6\cdot\left(-\frac{3}{4}\right)+b \\
1=-\frac{18}{4}+b \\
1=-4\frac{1}{2}+b \\
b=5\frac{1}{2}$$
To oznacza, że prosta \(BD\) wyraża się równaniem \(y=-\frac{3}{4}x+5\frac{1}{2}\).
Krok 4. Wyznaczenie współrzędnych przecięcia się przekątnych.
Z geometrycznej interpretacji układu równań wiemy, że rozwiązaniem układu równań zbudowanego z dwóch prostych jest miejsce ich przecięcia się, czyli dokładnie to, co nas interesuje. W związku z tym:
\begin{cases}
y=x-2 \\
y=-\frac{3}{4}x+5\frac{1}{2}
\end{cases}
Korzystając z metody podstawiania, otrzymamy
$$x-2=-\frac{3}{4}x+5\frac{1}{2} \\
\frac{7}{4}x=7\frac{1}{2} \\
\frac{7}{4}x=\frac{15}{2} \quad\bigg/\cdot\frac{4}{7} \\
x=\frac{60}{14}=4\frac{4}{14}=4\frac{2}{7}$$
Znając współrzędną \(x=4\frac{2}{7}\) możemy bez problemu wyznaczyć wartość współrzędnej \(y\). Podstawiając obliczony \(x\) np. do pierwszego równania, otrzymamy:
$$y=x-2 \\
y=4\frac{2}{7}-2 \\
y=2\frac{2}{7}$$
To oznacza, że przekątne przecinają się w punkcie \(S=\left(4\frac{2}{7};2\frac{2}{7}\right)\).