Rozwiązanie
Krok 1. Doprowadzenie nierówności do postaci ogólnej.
Zanim zaczniemy liczyć deltę, to musimy przenieść wszystkie wyrazy na lewą stronę, doprowadzając nierówność do postaci ogólnej, zatem:
$$x^2+5x\le6 \\
x^2+5x-6\le0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=1,\;b=5,\;c=-6\)
$$Δ=b^2-4ac=5^2-4\cdot1\cdot(-6)=25-(-24)=25+24=49 \\
\sqrt{Δ}=\sqrt{49}=7$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-5-7}{2\cdot1}=\frac{-12}{2}=-6 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-5+7}{2\cdot1}=\frac{2}{2}=1$$
Krok 3. Szkicowanie wykresu paraboli.
Z racji tego, iż współczynnik kierunkowy \(a\) jest dodatni, to parabola będzie mieć ramiona skierowane do góry. Zaznaczamy więc na osi wyznaczone miejsca zerowe \(x=-6\) oraz \(x=1\) (kropki będą zamalowane, bo w nierówności wystąpił znak \(\le\)) i rysujemy parabolę:
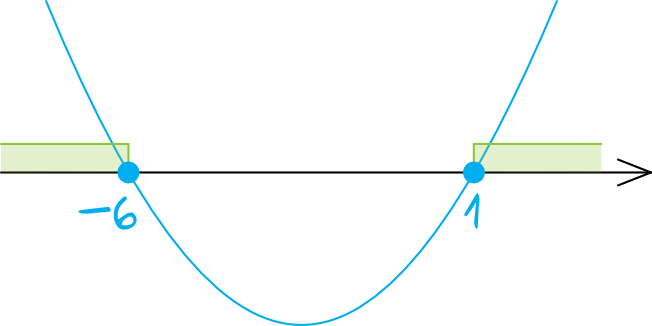
Krok 4. Odczytanie rozwiązania.
Interesują nas wyniki mniejsze lub równe zero, zatem interesuje nas to co znalazło się pod osią (wraz z zamalowanymi kropkami). To oznacza, że rozwiązaniem tej nierówności jest przedział:
$$x\in\langle-6;1\rangle$$