Objętość - Matematyka

Co to jest objętość?
Na matematyce już kilka razy zajmowaliśmy się różnymi pomiarami. Mierzyliśmy m.in. długość jakichś obiektów lub pole powierzchni danej figury. Dzisiaj poznamy pewne pomiary, które są związane z bryłami oraz przestrzenią, którą te bryły wypełniają. Rezultat tych pomiarów będziemy nazywać właśnie objętością.

Czym tak naprawdę jest objętość?
Wyobraź sobie, że jedziesz na wycieczkę i musisz spakować swój plecak lub walizkę. To ile zmieścisz do takiego plecaka lub walizki zależy od ich trzech wymiarów – wysokości, długości i szerokości. To właśnie kombinacja tych trzech parametrów decyduje o tym jaka jest objętość danej figury (w naszym przypadku torby lub plecaka). Z objętością spotkałeś się na pewno także w sklepie, gdzie kupując głównie napoje mamy informację o tym ile litrów soku znajduje się w danej butelce lub kartonie. Tym samym znasz już niektóre jednostki, którymi posługujemy się przy opisywaniu objętości – np. litr lub mililitr. Prawdopodobnie część z Was też wie, że jednostki objętości występują także na niektórych rachunkach domowych – np. zużycie wody i gazu mierzymy w metrach sześciennych ($m^3$) .

Przejdźmy teraz do konkretów. Spójrz na poniższy sześcian:

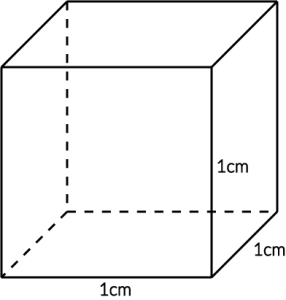
Przed chwilą powiedzieliśmy sobie, że o objętości decydują trzy parametry – wysokość, długość i szerokość bryły. W naszym sześcianie każdy z tych parametrów ma dokładnie $1cm$. To znaczy, że objętość naszej bryły wynosi dokładnie jeden centymetr sześcienny, który zapisujemy jako $1cm^3$.
$$V=1cm\cdot1cm\cdot1cm=1cm^3$$

Gdyby każda krawędź powyższego sześcianu miała długość $1m$, to taki sześcian miałby objętość jednego metra sześciennego ($1m^3$). Analogicznie byłoby w przypadku sześcianu o boku $1mm$ (jego objętość to $1mm^3$), $1dm$ (jego objętość to $1dm^3$), czy też $1km$ (jego objętość to $1km^3$).

Szczególnymi jednostkami, które na pewno znasz są litr i mililitr. Przyjęło się mówić, że objętość równa $1dm^3$ to $1$ litr ($1l$), a objętość $1cm^3$ to $1$ mililitr ($1ml$). Dodatkowo warto zapamiętać, że $1l=1000ml$.

W kolejnych działach nauczymy się obliczać objętość poszczególnych brył, w tym także tych, które nie są sześcianami. W tym momencie najważniejsze jest to, byś potrafił sobie wyobrazić czym tak naprawdę jest objętość, dlatego proponuję Ci proste ćwiczenie:

Zadania kontrolne:

Zadanie 1. Wymień dwa przedmioty lub dwa obiekty, których objętość najwygodniej byłoby podać w:
a) centymetrach sześciennych ($cm^3$)
b) metrach sześciennych ($m^3$)

Pamiętaj, że nie musi to być sześcian, ani nawet coś co ma regularne kształty.

Rozwiązanie

Odpowiedź: W centymetrach sześciennych ($cm^3$) moglibyśmy podać objętość np. butelki, szklanki, pudełka po butach, plecaka
W metrach sześciennych ($m^3$) podalibyśmy objętość np. garażu, mieszkania, wanny, basenu, szafy

Zadanie 2. Czy $1ml=0,001l$?

Rozwiązanie

Odpowiedź: Tak! Skoro $1l=1000ml$, to $1ml=0,001l$

Zadanie 3. Spróbuj narysować na kartce papieru dwa sześciany – jeden o boku $1cm$ i drugi o boku $2cm$. Skoro sześcian o boku $1cm$ ma objętość $1cm^3$, to czy sześcian o boku $2cm$ będzie miał $2cm^3$ objętości?

Rozwiązanie

Odpowiedź: Nie! W jednym z kolejnych działów dowiesz się jak należy obliczać objętość, ale już na podstawie tego prostego rysunku i wyobraźni przestrzennej powinieneś zauważyć, że objętość drugiego sześcianu będzie znacznie większa.

Z poniższych tematów dowiesz się jak należy obliczać objętość prostopadłościanu i sześcianu:

Objętość prostopadłościanu i sześcianu

Jednostki objętości

Oblicz objętość prostopadłościanu – ćwiczenie

Oblicz objętość ostrosłupa – ćwiczenie