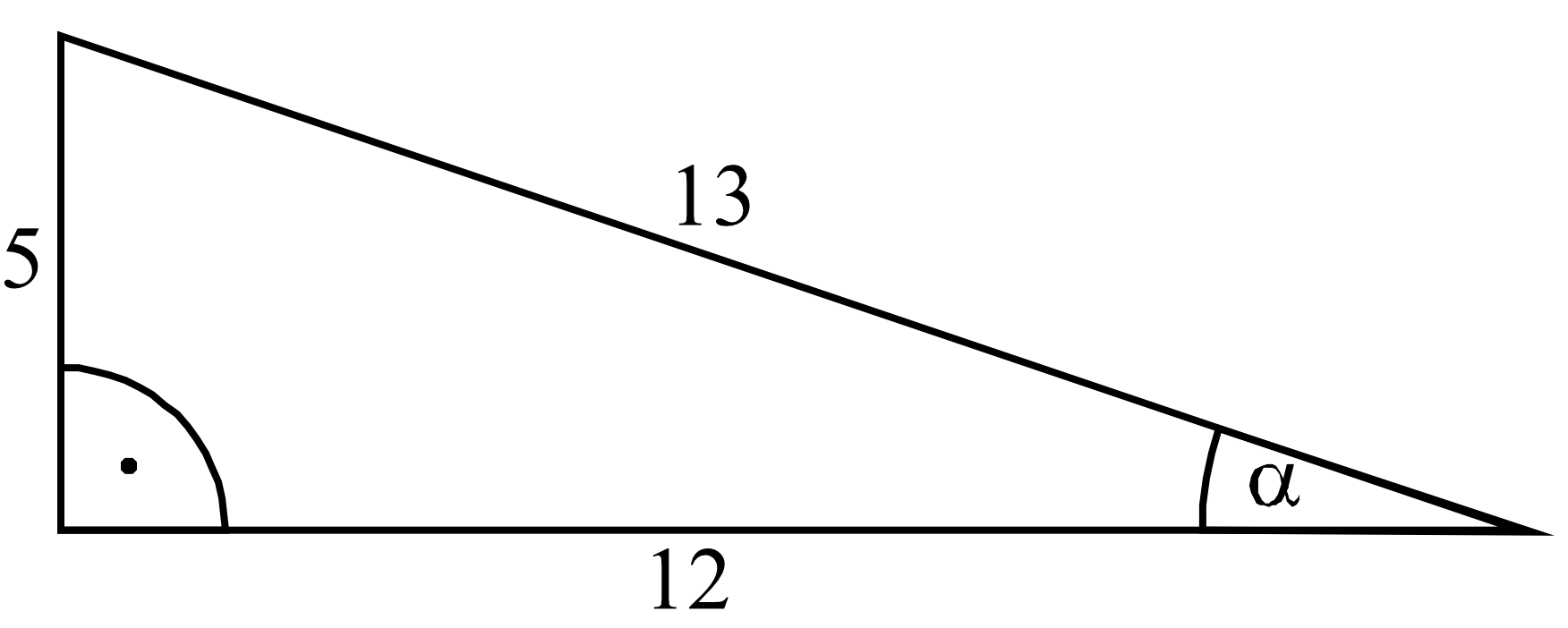
Na rysunku zaznaczono długości boków i kąt \(α\) trójkąta prostokątnego (zobacz rysunek). Wtedy:
\(cosα=\frac{5}{13}\)
\(tgα=\frac{13}{12}\)
\(cosα=\frac{12}{13}\)
\(tgα=\frac{12}{5}\)
Rozwiązanie:
Musimy obliczyć wartości \(cosα\) oraz \(tgα\), by sprawdzić która równość podana w odpowiedziach jest prawidłowa. Cosinus to stosunek długości przyprostokątnej leżącej przy kącie \(α\) do długości przeciwprostokątnej, natomiast tangens to stosunek długości przyprostokątnej leżącej naprzeciwko kąta \(α\) do długości przyprostokątnej leżącej przy kącie \(α\). Zatem:
$$cosα=\frac{12}{13} \\
tga=\frac{5}{12}$$
Porównujemy teraz otrzymane wyniki z tymi które występują w odpowiedziach i stwierdzamy, że prawdziwa równość jest zapisana tylko w punkcie \(C\).
Odpowiedź:
C. \(cosα=\frac{12}{13}\)

