Pole powierzchni całkowitej graniastosłupa

Pole powierzchni całkowitej to suma pól powierzchni wszystkich ścian danej bryły. W przypadku graniastosłupów będzie do suma pól dwóch podstaw (dolnej i górnej) oraz wszystkich ścian bocznych.

Wzór na pole powierzchni całkowitej zależy w dużej mierze od tego jaki to jest graniastosłup, ale w dużym uproszczeniu możemy zapisać, że:
$$P_{c}=2P_{p}+P_{b}$$

gdzie:
$P_{c}$ – pole powierzchni całkowitej
$P_{p}$ – pole podstawy
$P_{b}$ – pole powierzchni bocznej (czyli suma wszystkich pól ścian bocznych)

Warto też dodać, że jeżeli nasz graniastosłup jest prostopadłościanem, to jego pole powierzchni całkowitej możemy obliczyć alternatywnie ze wzoru:
$$P_{c}=2\cdot(ab+bc+ac)$$

gdzie:
$P_{c}$ – pole powierzchni całkowitej
$a, b, c$ – długości krawędzi prostopadłościanu

Przykład 1. Oblicz pole powierzchni całkowitej poniższego graniastosłupa.

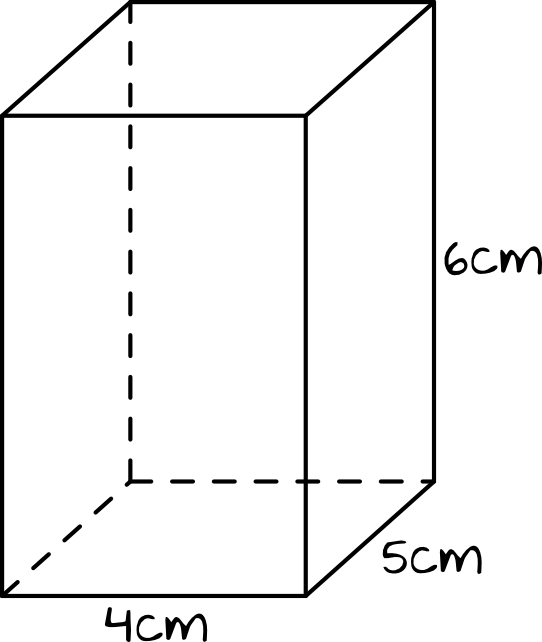
pole powierzchni całkowitej graniastosłupa

Rozwiązanie:
Nasz graniastosłup jest prostopadłościanem o wymiarach $4cm\times5cm\times6cm$. Pole powierzchni całkowitej możemy więc obliczyć korzystając zarówno z tego pierwszego, jak i z drugiego wzoru.

I sposób – z wykorzystaniem wzoru $P_{c}=2P_{p}+P_{b}$
W podstawie graniastosłupa mamy prostokąt o wymiarach $4cm\times5cm$, zatem:
$$P_{p}=4cm\cdot5cm \\
P_{p}=20cm^2$$

Jeżeli chodzi o ściany boczne, to dwie ściany będą mieć wymiary $4cm\times6cm$, a dwie będą mieć wymiary $5cm\times6cm$. Możemy więc zapisać, że:
$$P_{b}=2\cdot4cm\cdot6cm+2\cdot5cm\cdot6cm \\
P_{b}=48cm^2+60cm^2 \\
P_{b}=108cm^2$$

Znając pole podstawy oraz pole powierzchni bocznej jesteśmy już w stanie podać pole powierzchni całkowitej:
$$P_{c}=2P_{p}+P_{b} \\
P_{c}=2\cdot20cm^2+108cm^2 \\
P_{c}=40cm^2+108cm^2 \\
P_{c}=148cm^2$$

II sposób – z wykorzystaniem wzoru $P_{c}=2\cdot(ab+bc+ac)$
Nie ma co ukrywać, stosowanie tego wzoru jest znacznie prostsze, bo wystarczy podstawić $a=4cm$, $b=5cm$ oraz $c=6cm$ i otrzymamy:
$$P_{c}=2cdot(ab+bc+ac) \\
P_{c}=2\cdot(4cm\cdot5cm+5cm\cdot6cm+4cm\cdot6cm) \\
P_{c}=2\cdot(20cm^2+30cm^2+24cm^2) \\
P_{c}=2\cdot74cm^2 \\
P_{c}=148cm^2$$

Przykład 2. Oblicz wysokość graniastosłupa prawidłowego czworokątnego, którego krawędź podstawy jest równa $3$, a pole powierzchni całkowitej wynosi $78$.

Rozwiązanie:
Krok 1. Sporządzenie rysunku pomocniczego.
Obliczenia zacznijmy od prostego rysunku szkicowego, pamiętając o tym, że skoro graniastosłup jest prawidłowy czworokątny, to w podstawie musi znaleźć się kwadrat:

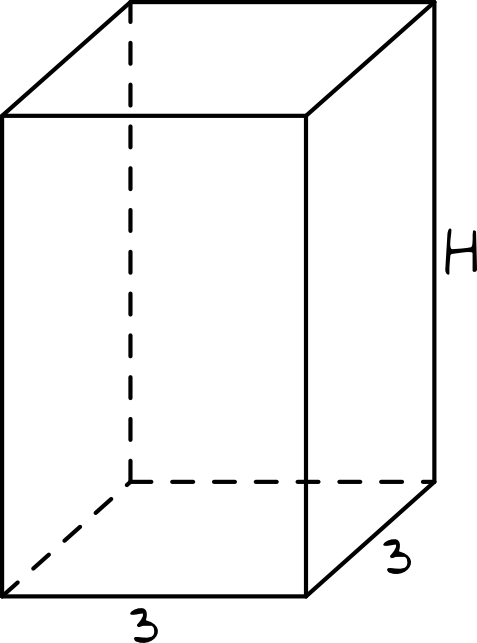
pole powierzchni całkowitej graniastosłupa

Krok 2. Obliczenie pól powierzchni podstaw.
W podstawie mamy kwadrat o boku $3$, zatem jego pole powierzchni będzie równe:
$$P_{p}=3\cdot3=9$$

W graniastosłupie mamy dwie podstawy (dolną i górną), zatem ich pola powierzchni łącznie wyniosą:
$$9+9=18$$

Krok 3. Obliczenie pola powierzchni bocznej.
Skoro pole powierzchni całkowitej jest równe $78$, a suma obydwu podstaw jest równa $18$, to pole powierzchni bocznej będzie równe:
$$P_{b}=78-18 \\
P_{b}=60$$

Krok 4. Obliczenie wysokości graniastosłupa.
Z rysunku jasno wynika, że ścianami bocznymi naszego graniastosłupa są cztery identyczne prostokąty. W każdym z tych prostokątów jeden bok ma długość $3$, a drugi bok jest wysokością całej bryły. Skoro więc suma pól powierzchni tych prostokątów ma być równa $60$, to:
$$4\cdot3\cdot H=60 \\
12H=60 \\
H=5$$

To oznacza, że wysokość naszej bryły jest równa $5$.

Zobacz też: Pole powierzchni całkowitej ostrosłupa

Zobacz też: Liczba ścian, krawędzi oraz wierzchołków graniastosłupa

Zobacz też: Objętość graniastosłupa