Funkcja liniowa \(f(x)=(m^2-4)x+2\) jest malejąca, gdy:
Funkcja jest malejąca wtedy, gdy jej współczynnik kierunkowy jest mniejszy od zera (czyli \(a\lt0\)). W tym przypadku współczynnik \(a\) został zapisany z parametrem, więc aby nasza funkcja była malejąca, to \(m^2-4\) musi być mniejsze od zera.
Aby dowiedzieć się kiedy funkcja jest malejąca musimy rozwiązać nierówność \(m^2-4\lt0\). Możemy ją oczywiście obliczyć za pomocą delty lub zapisując ją w postaci iloczynowej, ale tak naprawdę jest to prosta nierówność, którą śmiało możemy rozwiązać w pamięci. Rozwiązaniem tej nierówności jest oczywiście przedział \(m\in(-2;2)\). Jeśli jednak nie umiemy tego wyliczyć w pamięci, to możemy rozwiązać to jak każdą inną nierówność w trzech prostych krokach:
1. Najpierw szukamy miejsc zerowych, więc przyrównujemy \(m^2-4\) do zera:
$$m^2-4=0 \\
(m-2)(m+2)=0 \\
m=2 \quad\lor\quad m=-2$$
2. Następnie rysujemy szkic paraboli. Ramiona paraboli będą skierowane ku górze, bo przed \(m^2\) nie stoi znak minusa:
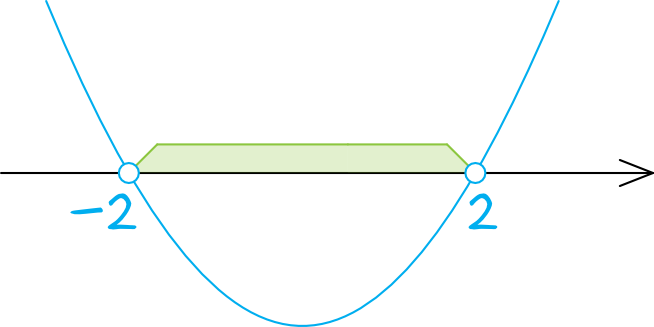
3. Teraz odczytujemy dla jakich wartości funkcja przyjmuje wartości ujemne (czyli dla jakich argumentów wykres funkcji znalazł się pod osią \(Ox\)), a jest to przedział \(m\in(-2;2)\).
B. \(m\in(-2;2)\)


funkcja liniowa i parabola?
Parabola jest do nierówności kwadratowej, którą rozwiązujemy, aby poznać rozwiązanie zadania ;)
Czy w tym zadaniu nie była by też poprawna odpowiedz C) m∈(−∞;−2)
No nie, bo przykładowo dla m=-100 funkcja nie będzie malejąca ;)
A przypadkiem funkcja malejąca to nie jest coś innego niż ujemna? Tzn idzie na dół a nie jest na -…
No zgadza się, ale będzie ona szła w dół tylko wtedy, gdy ten współczynnik a będzie ujemny ;) I celem zadania jest właśnie określenie kiedy tak się stanie.