Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Aby mieć pełen obraz tej sytuacji, to warto zrobić sobie nawet prosty rysunek szkicowy.
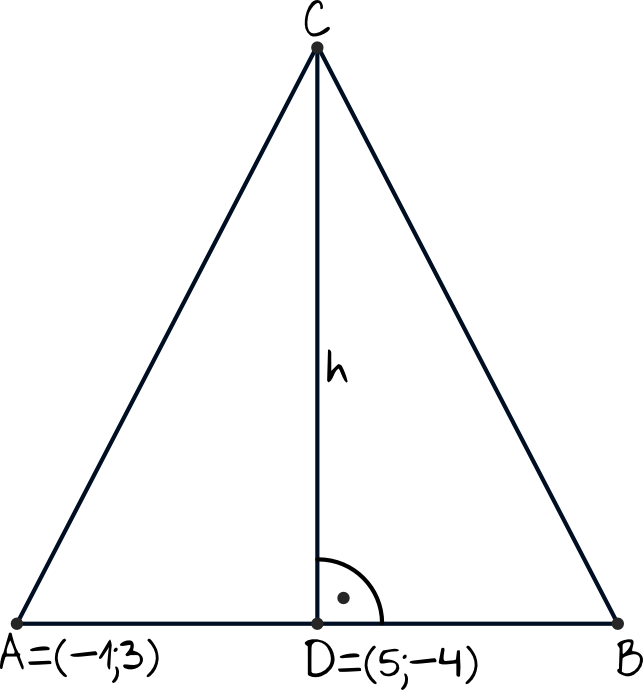
Jedną z własności trójkąta równoramiennego jest to, że jego wysokość \(CD\) dzieli nam podstawę na dwie równe części. Można więc powiedzieć, że punkt \(D\) jest środkiem odcinka \(AB\).
Krok 2. Wyznaczenie współrzędnych wierzchołka \(B\).
Środek odcinka \(AB\) o współrzędnych \(A=(x_{A};y_{A})\) oraz \(B=(x_{B};y_{B})\) możemy opisać wzorem:
$$D=\left(\frac{x_{A}+x_{B}}{2};\frac{y_{A}+y_{B}}{2}\right)$$
Znamy współrzędne punktu \(A\) oraz \(D\), zatem jedyną niewiadomą zostają poszukiwane współrzędne punktu \(B\). Dla przejrzystości obliczeń możemy je wyznaczyć oddzielnie:
$$x_{D}=\frac{x_{A}+x_{B}}{2} \\
5=\frac{-1+x_{B}}{2} \\
10=-1+x_{B} \\
x_{B}=11 \\
\quad \\
y_{D}=\frac{y_{A}+y_{B}}{2} \\
-4=\frac{3+y_{B}}{2} \\
-8=3+y_{B} \\
y_{B}=-11$$
To oznacza, że \(B=(11;-11)\).