Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
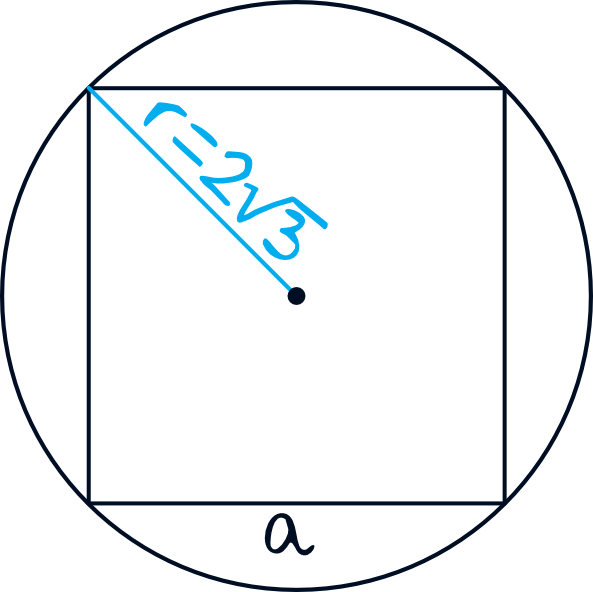
Z rysunku wynika, że długość promienia jest jednocześnie połową długości przekątnej kwadratu. Ta obserwacja pozwoli nam obliczyć długość boku.
Krok 2. Obliczenie długości boku kwadratu.
Skoro połowa przekątnej kwadratu jest równa \(2\sqrt{3}\), to cała przekątna ma długość:
$$d=2\cdot2\sqrt{3} \\
d=4\sqrt{3}$$
Z własności kwadratów wiemy, że kwadrat o boku długości \(a\) ma przekątną długości \(a\sqrt{2}\). Nasza przekątna ma długość \(4\sqrt{3}\), zatem:
$$a\sqrt{2}=4\sqrt{3} \quad\bigg/:\sqrt{2} \\
a=\frac{4\sqrt{3}}{\sqrt{2}} \\
a=\frac{4\sqrt{3}\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
a=\frac{4\sqrt{6}}{2} \\
a=2\sqrt{6}$$