W trójkącie prostokątnym ABC na boku AB obrano punkt D oddalony od punktu A o 6

W trójkącie prostokątnym $ABC$ na boku $AB$ obrano punkt $D$ oddalony od punktu $A$ o $6$ i od punktu $B$ o $4$. Przez punkt $D$ poprowadzono prostą równoległą do boku $AC$, przecinającą bok $BC$ w punkcie $E$. Oblicz długość odcinka $DE$.

Rozwiązanie

Krok 1. Sporządzenie rysunku pomocniczego.
W zadaniu jest sporo informacji, więc spróbujmy je przedstawić na rysunku pomocniczym:

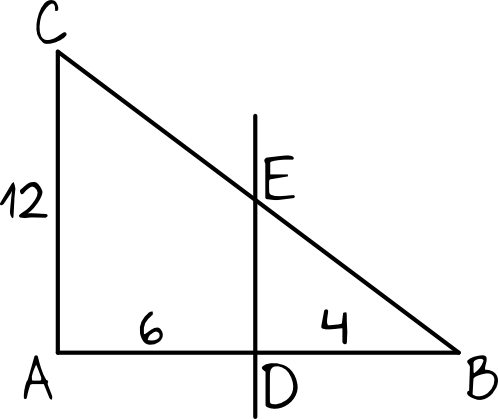
matura z matematyki

Krok 2. Zapisanie i rozwiązanie proporcji.
Musimy zauważyć, że trójkąty $DBE$ oraz $ABC$ są trójkątami podobnymi, a skoro tak to możemy ułożyć odpowiednią proporcję, która pozwoli nam odnaleźć długość odcinka $DE$.
$$\frac{|AB|}{|AC|}=\frac{|DB|}{|DE|} \\
\frac{10}{12}=\frac{4}{|DE|}$$

Mnożąc na krzyż otrzymamy:
$$10\cdot|DE|=48 \\
|DE|=4,8$$

Odpowiedź

$|DE|=4,8$

Zadania

W trójkącie prostokątnym ABC na boku AB obrano punkt D oddalony od punktu A o 6

W trójkącie prostokątnym \(ABC\) na boku \(AB\) obrano punkt \(D\) oddalony od punktu \(A\) o \(6\) i od punktu \(B\) o \(4\). Przez punkt \(D\) poprowadzono prostą równoległą do boku \(AC\), przecinającą bok \(BC\) w punkcie \(E\). Oblicz długość odcinka \(DE\).