Rozwiązanie
Krok 1. Obliczenie miejsc zerowych wielomianu.
Nasza nierówność podana jest w wygodnej formie iloczynowej, zatem aby obliczyć jej miejsca zerowe wystarczy przyrównać wartości znajdujące się w nawiasach do zera. Otrzymamy zatem:
$$x+3=0 \quad\lor\quad x-5=0 \\
x=-3 \quad\lor\quad x=5$$
Krok 2. Szkicowanie wykresu.
Nierówność jest nierównością trzeciego stopnia (to nie jest nierówność kwadratowa!), zatem jej wykresem nie będzie zwykła parabola, tylko linia tego typu:
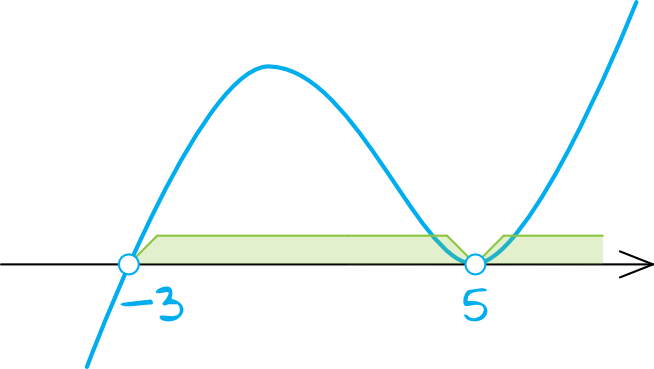
Krok 3. Odczytanie rozwiązania.
Interesują nas argumenty, dla których nierówność przyjmuje wartości większe od zera. W związku z tym: \(x\in(-3;5)\cup(5;+\infty)\).