Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Wielokąty. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) W którym zestawie figur wszystkie wypisane figury mają tę własność, że przekątne przecinają się w połowie swojej długości?
Zadanie 2. (1pkt) Dany jest trójkąt równoboczny \(ABC\) którego boki mają długość \(12\). Wysokości tego trójkąta przecinają się w punkcie \(S\). Jaka jest długość odcinka \(AS\)?
Zadanie 3. (1pkt) 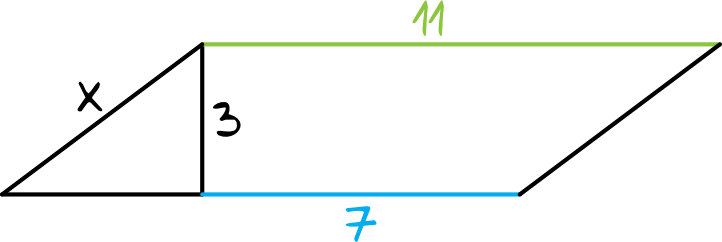
Długość boku \(x\) powyższego równoległoboku jest równa:
Zadanie 4. (1pkt) Który z podanych trójkątów jest trójkątem prostokątnym?
Zadanie 5. (1pkt) Przekątne rombu mają długości \(8\) oraz \(16\). W związku z tym bok tego rombu ma długość:
Zadanie 6. (1pkt) 
W powyższym trapezie znajdziemy kąt o mierze \(120°\).
Zadanie 7. (1pkt) Jeżeli przekątna kwadratu ma długość \(8\), to bok kwadratu ma długość \(4\sqrt{2}\).
Zadanie 8. (1pkt) Jaś twierdzi, że ośmiokąt foremny ma sumę kątów wewnętrznych równą \(8\cdot180°=1440°\), a każdy inny ośmiokąt będzie mieć sumę kątów mniejszą niż \(1440°\). Małgosia uważa, że niezależnie od tego czy ośmiokąt jest foremny czy też nie, to suma miar kątów wewnętrznych będzie równa \(6\cdot180°=1080°\). Kto ma rację?
Zadanie 9. (1pkt) Dany jest trójkąt prostokątny o przyprostokątnej \(5\sqrt{2}\) oraz przeciwprostokątnej \(2\sqrt{17}\). W związku z tym prawdą jest, że:
Zadanie 10. (1pkt) Trapez równoramienny ma długości boków równe \(\sqrt{7}, \sqrt{7}, 3, 7\). Długość przekątnej tego trapezu jest równa: