Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości \(2\), a przekątna ściany bocznej ma długość \(3\) (zobacz rysunek). Kąt, jaki tworzą przekątne ścian bocznych tego graniastosłupa wychodzące z jednego wierzchołka, ma miarę \(α\).
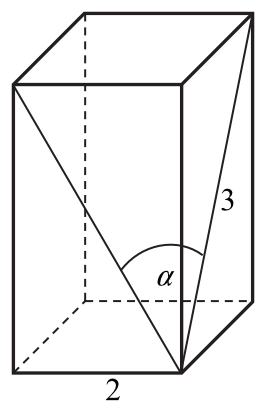
Wtedy wartość \(sin\frac{α}{2}\) jest równa:
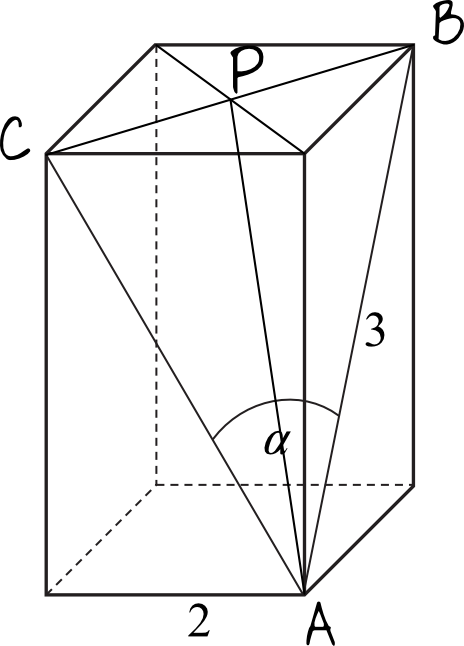
Pierwszą rzeczą którą musimy zauważyć, to że trójkąc \(ABC\) jest równoramienny. Jego ramiona mają długość \(3\), a podstawa jest równa \(|CB|=2\sqrt{2}\). Skąd wiemy, że to jest dokładnie taka długość podstawy? Jest to po prostu przekątna kwadratu o boku \(2\).
Jeżeli z miejsca przecięcia się tych przekątnych (punkt \(P\)) poprowadzimy prostą do wierzchołka \(A\) to otrzymamy tak naprawdę dwusieczną kąta \(α\) (bo jest to wysokość trójkąta równoramiennego, a ta dzieli kąt na dwie równe części). Mamy więc już interesujący nas kąt \(\frac{α}{2}\).
Obliczenia dokonujemy już tylko na trójkącie \(PCA\). Potrzebujemy wyznaczyć sinusa kąta \(CAP\), który ma miarę \(\frac{α}{2}\). Znamy potrzebną nam długosć \(|CA|=3\), potrzebujemy jeszcze poznać długość odcinka \(|CP|\). Jest to połowa przekątnej kwadratu, tak więc:
$$|CP|=\frac{2\sqrt{2}}{2}=\sqrt{2}$$
Możemy już teraz obliczyć pożądaną wartość sinusa:
$$sin\frac{α}{2}=\frac{|CP|}{|CA|} \\
sin\frac{α}{2}=\frac{\sqrt{2}}{3}$$
D. \(\frac{\sqrt{2}}{3}\)

