Na prostej o równaniu \(y=ax+b\) leżą punkty \(K=(1,0)\) i \(L=(0,1)\). Wynika stąd, że:
\(a=-1\) i \(b=1\)
\(a=1\) i \(b=-1\)
\(a=-1\) i \(b=-1\)
\(a=1\) i \(b=1\)
Rozwiązanie:
Krok 1. Określenie współczynnika \(a\).
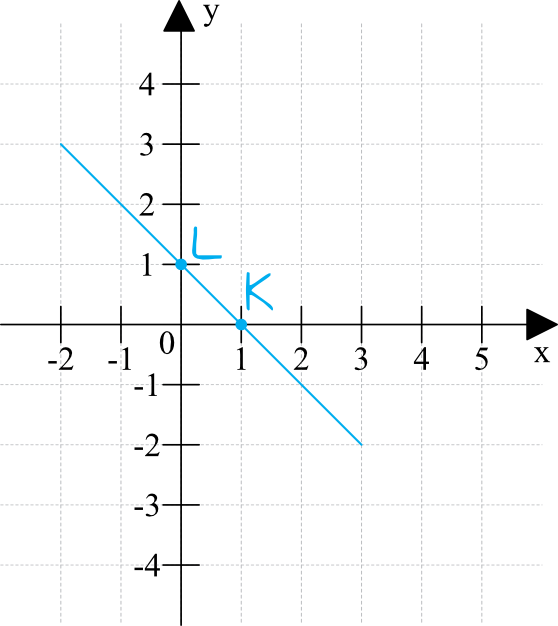
Z rysunku wynika, że nasza funkcja jest malejąca, tak więc współczynnik \(a\) jest na pewno mniejszy od zera. To oznacza, że prawidłową odpowiedzią jest \(A\) lub \(C\).
Krok 2. Określenie współczynnika \(b\).
Tu z pomocą przyjdą nam współrzędne punktu \(L\). Miejsce przecięcia się prostej z osią \(Oy\) mówi nam o tym jaka jest wartość współczynnika \(b\). Skoro prosta przecina oś \(Oy\) w punkcie \(L=(0,1)\), to \(b=1\).
Prawidłowa jest więc odpowiedź \(A\).
Odpowiedź:
A. \(a=-1\) i \(b=1\)

