Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Funkcja kwadratowa. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Która z poniższych funkcji kwadratowych będzie mieć ramiona paraboli skierowane do dołu?
Zadanie 2. (1pkt) Funkcja \(f(x)=3(x-2)^2-5\) ma swój wierzchołek w punkcie:
Zadanie 3. (1pkt) Która z tych funkcji kwadratowych przechodzi przez punkt \(A=(0;-4)\) oraz ma miejsce zerowe \(x_{0}=1\)?
Zadanie 4. (1pkt) Pewna funkcja kwadratowa ma jedno miejsce zerowe \(x_{0}=4\) oraz przechodzi przez punkt \(A=(1;5)\). W związku z tym prawdą jest, że:
Zadanie 5. (1pkt) Funkcja \(f(x)=2x^2-5x+2\) zapisana w postaci kanonicznej przybierze formę:
Zadanie 6. (1pkt) Pewna funkcja kwadratowa przyjmuje najmniejszą wartość równą \(-3\) i ma dwa miejsca zerowe: \(x=2\) oraz \(x=6\). To oznacza, że wierzchołek tej paraboli jest w punkcie \(W=(4;-3)\).
Zadanie 7. (1pkt) 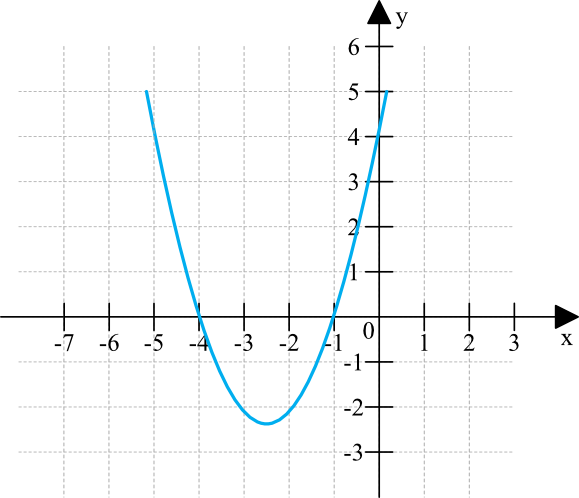
Wzorem powyższej funkcji jest \(f(x)=(x-4)(x-1)\).
Zadanie 8. (1pkt) Zdaniem Jasia wykres funkcji kwadratowej \(y=-2x^2+\sqrt{2}\) znajduje się w całości pod osią iksów, a tym samym parabola nie przetnie nigdy osi iksów. Małgosia uważa, że ten wykres przecina oś iksów i to jeszcze w dwóch miejscach. Kto ma rację?
Zadanie 9. (1pkt) Dla jakiego parametru \(a\) funkcja \(f(x)=ax^2+8x+4\) nie ma miejsc zerowych?
Zadanie 10. (1pkt) Jaką najmniejszą wartość przyjmuje funkcja \(y=(x+1)(x-7)\) dla argumentów z przedziału \(x\in\langle-2;6\rangle\)?

Jak obliczyć zadanie 8?
Jak skończysz test, to możesz go sobie później przejrzeć i zobaczyć poprawną odpowiedź wraz z pełnym wyjaśnieniem :)
Super