W tym temacie dowiemy się jak wykonać poprawnie dodawanie ułamków dziesiętnych (zarówno w pamięci jak i pisemnie), a także zwrócimy sobie uwagę na przykłady w których łatwo jest popełnić błąd.
Na poniższym rysunku mamy płot, w którym trzy szczeble pomalowane są na zielono, a pięć ma kolor niebieski. Pozostałe dwa szczeble czekają na pomalowanie. Odpowiedzmy sobie na pytanie: Jaką część płotu (wyrażoną w ułamku dziesiętnym) stanowią szczeble, które są już pomalowane?
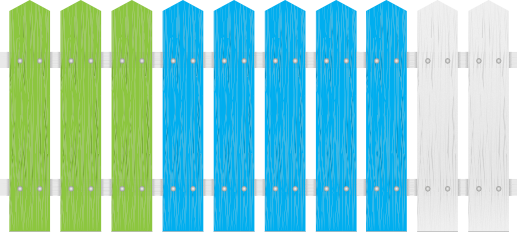
Zanim odpowiemy na pytanie, to wypiszmy sobie wszystko to, co wiemy o naszym płocie:
- Trzy szczeble (z dziesięciu, które są w płocie) pomalowane są na zielono, co stanowi \(0,3\) całego płotu.
- Pięć szczebli jest pomalowanych na niebiesko, co z kolei stanowi \(0,5\) całego płotu.
- Chcąc wiedzieć jaka część płotu jest pomalowana powinniśmy więc dodać do siebie \(0,3+0,5=\)…
Nawet nie znając jeszcze dodawania ułamków dziesiętnych jesteśmy w stanie określić wynik tego działania, bo widzimy na rysunku, że \(8\) z \(10\) szczebli jest już pomalowanych, co oznacza że pomalowano już \(0,8\) całego płotu. Z powyższej rozpiski możemy wywnioskować, że \(0,3+0,5=0,8\).
Powyższe zadanie było dość proste, ale na jego podstawie musimy dostrzec, że istnieje spore podobieństwo działania \(0,3+0,5=0,8\) do bardzo prostego dodawania \(3+5=8\) i właśnie to będziemy wykorzystywali przy dodawaniu ułamków dziesiętnych.
Spójrzmy na kilka przykładów dodawania ułamków dziesiętnych, które możemy wykonać w pamięci:
$$0,1+0,7=0,8 \\
0,11+0,71=0,82 \\
0,1+0,9=1 \\
1,25+1,13=2,38$$
W każdym z powyższych przykładów mieliśmy sytuację w której dodawane ułamki dziesiętne miały taką samą liczbę cyfr po przecinku. A co w przypadku, kiedy jeden ułamek ma np. jedną cyfrę po przecinku, a drugi będzie miał dwie lub trzy cyfry? Nic nie stoi na przeszkodzie, by do tej liczby która ma mniej cyfr po przecinku dopisać sobie zera:
$$0,1+0,75=0,10+0,75=0,85 \\
0,1+0,234=0,100+0,234=0,334 \\
54+1,13=54,00+1,13=55,13$$
Powyższe działania nie były zbyt skomplikowane. Zdarzają się jednak także takie przykłady, które dość trudno oblicza się w pamięci (zwłaszcza jeśli dopiero uczymy się tego zagadnienia). Wtedy z pomocą może przyjść dodawanie pisemne ułamków dziesiętnych:
Krok 1. Aby dobrze wykonać dodawanie pisemne ułamków dziesiętnych musimy pamiętać o jednej istotnej sprawie – ułamki dziesiętne musimy zapisać w taki sposób, by przecinki z ułamków które dodajemy znalazły się w jednej linii. W razie konieczności możemy dopisać zera w pustych miejscach na końcu każdego ułamka. Chcąc więc dodać do siebie np. \(3,743\) i \(4,5\) musimy zrobić to w następujący sposób:
$$\quad \quad 3,743 \\
+\quad 4,5\color{blue}{00} \\
\overline {\quad \quad \quad \quad}$$
Teraz dodajemy praktycznie tak samo, jakbyśmy dodawali do siebie \(3743\) i \(4500\), z tą tylko różnicą, że w wyniku pojawi się nam przecinek.
Krok 2. Na początku dodajemy \(3+0\), co daje nam wynik równy \(3\).
$$\quad \quad 3,743 \\
+\quad 4,5\color{blue}{00} \\
\overline {\quad \quad \quad \quad 3}$$
Krok 3. Teraz \(4+0=4\)
$$\quad \quad 3,743 \\
+\quad 4,5\color{blue}{00} \\
\overline {\quad \quad \quad \;\; 43}$$
Krok 4. I teraz najtrudniejszy moment, który pojawiał się także w tradycyjnym dodawaniu pisemnym. \(7+5=12\), więc zapisujemy pod kreską dodawania cyfrę \(2\), a jedynkę przenosimy (w pamięci lub na kartce) na lewą stronę:
$$\quad 1 \quad \\
\quad \quad 3,743 \\
+\quad 4,5\color{blue}{00} \\
\overline {\quad \quad \quad 243}$$
Krok 5. Na koniec dodajemy \(1+3+4=8\)
$$\quad 1 \quad \\
\quad \quad 3,743 \\
+\quad 4,5\color{blue}{00} \\
\overline {\quad \quad 8\;243}$$
Krok 6. Jedyne co nam pozostało, to postawić przecinek pod pozostałymi przecinkami:
$$\quad 1 \quad \\
\quad \quad 3,743 \\
+\quad 4,5\color{blue}{00} \\
\overline {\quad \quad 8,243}$$
I już wiemy, że wynikiem dodawania \(3,743+4,5\) jest \(8,243\)
Na koniec powiedzmy sobie o jeszcze jednej możliwości dodawania ułamków dziesiętnych – jeśli nie czujemy się zbyt pewnie w temacie dodawania ułamków dziesiętnych (albo chcemy się upewnić na sprawdzianie, czy na pewno dobrze wszystko policzyliśmy), to zawsze awaryjnie możemy zamienić ułamki dziesiętne na ułamki zwykłe, np.:
$$0,1+0,7=\frac{1}{10}+\frac{7}{10}=\frac{1+7}{10}=\frac{8}{10}=0,8 \\
\quad \\
0,15+0,7=\frac{15}{100}+\frac{70}{100}=\frac{15+70}{100}=\frac{85}{100}=0,85$$
Jeśli chcesz poćwiczyć dodawanie ułamków dziesiętnych lub też poznać inne działania, to zapraszam Cię do poniższych tematów:

Bardzo dziękuje pani z szkoły która nam tę stronę polecała. Bardzo dobre tłumaczenie
Też się z Tobą zgadzam jest bardzo pomocna
Do nauki na sprawdzian w sam raz
Bardzo dobrze tłumaczysz różne zagadnienia, to moja ulubiona strona do nauki matematyki :)
Dzięki za świetne wyjaśnienie
Dzięki za wyjaśnienie
to moja ulubiona strona do matematyki
fajne objaśnienia i ćwiczenia i mogę równocześnie mieć włączonego librusa
dobra strona polecam
To jest dość proste ale i tak naprawdę dobre tłumaczenie
Dziękuje za wyjaśnienie :)
DZIĘKI
Dziękuję Ci, bardzo dobre tłumaczenie, da się zrozumieć
Bardzo fajna strona polecam do nauki np. na sprawdziany czy po prostu dla przypomnienia tematu
mega stronka wytłumaczyła mi różne tematy
Fajna stronka polecam dużo możecie się dowiedzieć o ułamkach dziesiętnych!:)
Polecam tę stronę na maaaaaksa
Wreszcie rozumiem
Byłem chory i nie chodziłem do szkoły a dzięki tej stronie szybko nadrobiłem tematy z matematyki