Rozwiązanie
Krok 1. Odczytanie współrzędnych wierzchołka paraboli.
Nasza funkcja zapisana jest w postaci kanonicznej \(f(x)=a(x-p)^2+q\). Z tej postaci odczytamy współrzędne wierzchołka paraboli \(W=(p;q)\), co pozwoli nam za chwilę udzielić odpowiedzi na pytanie o najmniejszą/największą wartość. Aby dobrze odczytać te współrzędne możemy sobie przekształcić wzór funkcji w taki oto sposób:
$$f(x)=-3(x-2)^2-5 \\
f(x)=-3(x-2)^2+(-5)$$
Teraz wyraźnie widać, że \(p=2\) oraz \(q=-5\).
Krok 2. Sporządzenie rysunku pomocniczego.
Funkcja ma współczynnik \(a\) ujemny (\(a=-3\)), więc ramiona paraboli będą skierowane do dołu. Możemy zatem szkicowo narysować sobie, że cała sytuacja będzie wyglądać następująco:
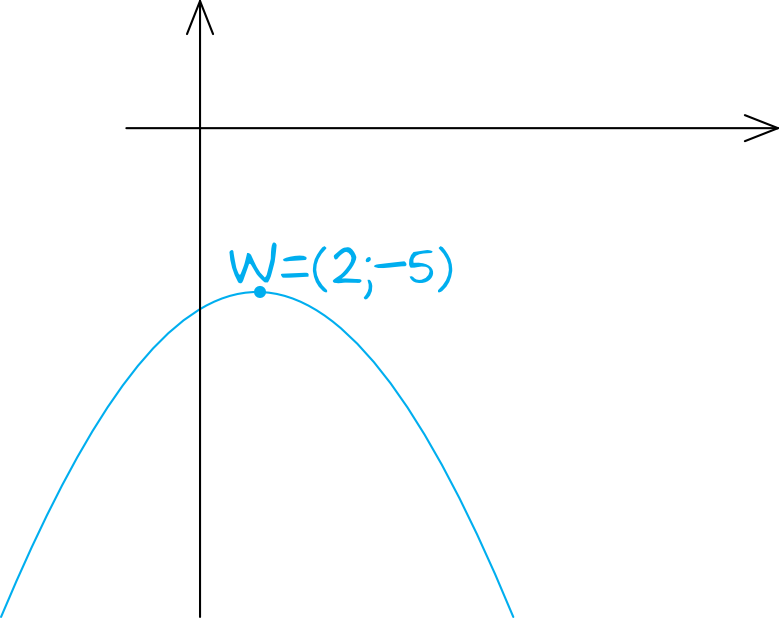
To oznacza, że prawidłową odpowiedzią będzie informacja, że największa wartość tej funkcji jest równa \(-5\).