Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować nasz trójkąt \(ABC\) i zaznaczmy na nim dane z treści zadania:
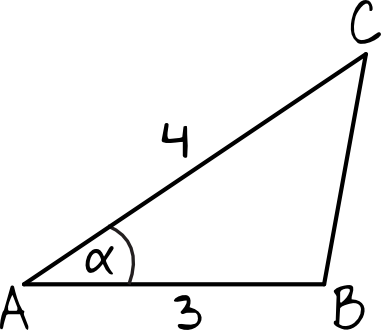
Zwróć uwagę, że to nie będzie trójkąt prostokątny (bok \(BC\) nie będzie miał długości \(5\)). W związku z tym, do obliczenia pola powierzchni tego trójkąta przyda nam się tak zwany "wzór z sinusem", czyli:
$$P=\frac{1}{2}ab\cdot sin\alpha$$
Krok 2. Obliczenie \(sin\alpha\).
Do obliczenia pola potrzebujemy znać wartość sinusa kąta \(\alpha\), a znamy cosinusa. Aby poznać wartość sinusa tego kąta, możemy skorzystać z jedynki trygonometrycznej:
$$sin^2\alpha+cos^2\alpha=1 \\
sin^2\alpha+\left(\frac{4}{5}\right)^2=1 \\
sin^2\alpha+\frac{16}{25}=1 \\
sin^2\alpha=\frac{9}{25} \\
sin\alpha=\frac{3}{5} \quad\lor\quad sin\alpha=-\frac{3}{5}$$
Zarówno kąty ostre jak i rozwarte (a takimi mogłaby być nasza \(\alpha\)) są dodatnie, więc jedynym pasującym rozwiązaniem jest \(sin\alpha=\frac{3}{5}\).
Krok 3. Obliczenie pola powierzchni.
Korzystając ze wzoru na pole trójkąta "z sinusem", otrzymamy:
$$P=\frac{1}{2}ab\cdot sin\alpha \\
P=\frac{1}{2}\cdot3\cdot4\cdot\frac{3}{5} \\
P=6\cdot\frac{3}{5} \\
P=\frac{18}{5}$$