Punkt \(K=(-4,4)\) jest końcem odcinka \(KL\), punkt \(L\) leży na osi \(Ox\), a środek \(S\) tego odcinka leży na osi \(Oy\). Wynika stąd, że:
W zasadzie wykonując dokładny rysunek moglibyśmy odczytać z niego rozwiązanie, bez dokonywania jakichkolwiek obliczeń.
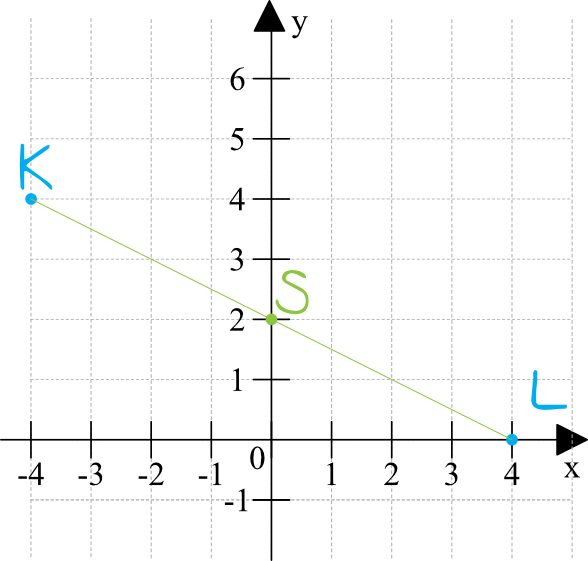
Nawet gdybyśmy zrobili tylko szkic tej sytuacji, to po prostej analizie odpowiedzi możemy odrzucić \(B\) oraz \(C\), bo pierwszą współrzędną punktu \(S\) jest na pewno \(0\) (wiemy to, bo zgodnie z treścią zadania punkt ten leży na osi \(Oy\)). W zasadzie to i odpowiedź \(D\) możemy odrzucić, bo punkt \(S\) jest na pewno niżej położony niż punkt \(K\), więc druga współrzędna (igrekowa) musi być mniejsza od \(4\). W ten oto sposób wiemy już, że to musi być odpowiedź \(A\).
Nie mniej jednak spróbujmy to obliczyć, bo mogłyby tutaj znaleźć się znacznie bardziej skomplikowane liczby (np. z pierwiastkami). Ustalmy zatem jakie znamy współrzędne:
$$K=(-4;4) \\
L=(x_{L};0) \\
S=(0;y_{S})$$
Naszym zadaniem jest podanie współrzędnych punktu \(S\), zatem brakuje nam współrzędnej \(y_{S}\). Do wyznaczenia brakującej współrzędnej wykorzystamy wzór na środek odcinka.
Ze wzoru na środek odcinka wiemy, że:
$$x_{S}=\frac{x_{K}+x_{L}}{2} \\
y_{S}=\frac{y_{K}+y_{L}}{2}$$
Nas interesuje tylko współrzędna „igrekowa”, bo „iksową” już znamy, zatem:
$$y_{S}=\frac{y_{K}+y_{L}}{2} \\
y_{S}=\frac{4+0}{2} \\
y_{S}=2$$
To oznacza, że poszukiwane współrzędne to \(S=(0;2)\).
A. \(S=(0,2)\)

