Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Sytuacja z treści zadania wygląda następująca:
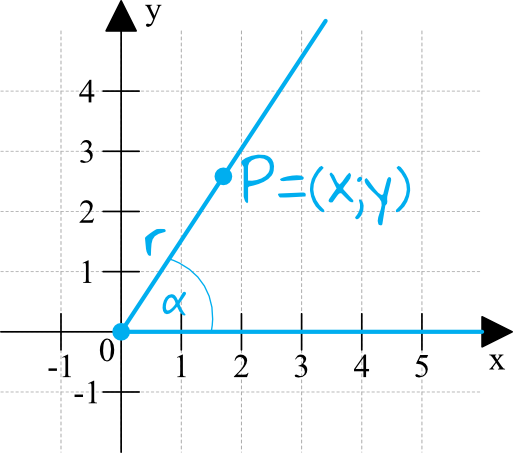
Kluczem do sukcesu jest pamiętanie o tym, że w tej konkretnej sytuacji (gdy jedno ramię kąta pokrywa się z osią \(OX\), a wierzchołek jest w punkcie będącym początkiem układu współrzędnych), możemy skorzystać ze wzorów na sinusa, cosinusa oraz tangensa w układzie współrzędnych (które znajdują się w tablicach). Nas interesuje cosinus, zatem interesuje nas wzór \(cos=\frac{x}{r}\), gdzie \(x\) jest współrzędną \(x\) dowolnego punktu na górnym ramieniu kąta, a \(r\) to odległość od wierzchołka do tego punktu (patrz rysunek).
Możemy więc wywnioskować, że skoro \(cos\alpha=\frac{\sqrt{3}}{3}\), to \(x=\sqrt{3}\) oraz \(r=3\).
Krok 2. Obliczenie współrzędnej \(y\) punktu \(P\).
Aby obliczyć współczynnik kierunkowy prostej \(k\), musimy jeszcze poznać współrzędną \(y\) punktu \(P\). W tym celu możemy skorzystać z Twierdzenia Pitagorasa:
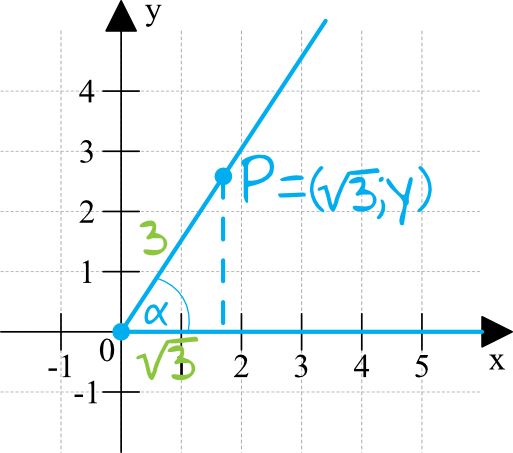
$$(\sqrt{3})^2+y^2=3^2 \\
3+y^2=9 \\
y^2=6 \\
y=\sqrt{6}$$
To oznacza, że \(P=(\sqrt{3};\sqrt{6})\).
Krok 3. Wyznaczenie współczynnika kierunkowego \(a\).
Do wyznaczenia współczynnika kierunkowego \(a\) potrzebujemy współrzędnych dwóch punktów, które należą do danej prostej. U nas takimi punktami będą wierzchołek znajdujący się w punkcie \(A=(0;0)\) oraz obliczony punkt \(P=(\sqrt{3};\sqrt{6})\). W związku z tym:
$$a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}} \\
a=\frac{\sqrt{6}-0}{\sqrt{3}-0} \\
a=\frac{\sqrt{6}}{\sqrt{3}} \\
a=\sqrt{2}$$