Dany jest trapez \(ABCD\), w którym przekątna \(AC\) jest prostopadła do ramienia \(BC\), \(|AD|=|DC|\) oraz \(|\sphericalangle ABC|=50°\) (zobacz rysunek).
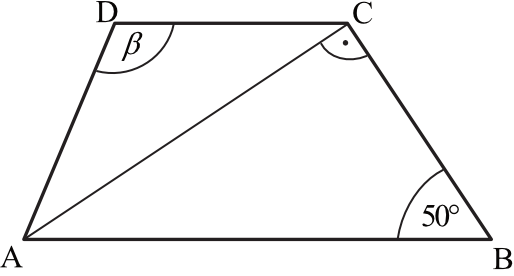
Stąd wynika, że:
\(β=100°\)
\(β=120°\)
\(β=110°\)
\(β=130°\)
Rozwiązanie:
Krok 1. Obliczenie miary kąta \(CAB\).
Z trójkąta \(ABC\) jesteśmy wyznaczyć miarę kąta \(CAB\):
$$|\sphericalangle CAB|=180°-90°-50°=40°$$
Krok 2. Obliczenie miary kątów \(ACD\) oraz \(DAC\).
Musimy zauważyć, że kąty \(ACD\) i \(DAC\) będą miały równą miarę. Skąd to wiemy? Wynika to z tego, że \(|AD|=|DC|\), co sugeruje nam że trójkąt \(ACD\) jest równoramienny, a w takim trójkącie kąty przy podstawie są równej miary.
Z własności kątów naprzemianległych wiemy, że kąty \(CAB\) oraz \(ACD\) mają równą miarę. W związku z tym:
$$|\sphericalangle CAB|=|\sphericalangle ACD|=|\sphericalangle DAC|=40°$$
Krok 3. Obliczenie miary kąta \(ADC\) (czyli \(β\)).
Znając kąty \(ACD\) i \(DAC\) bez problemu wyliczymy miarę naszego kąta \(β\):
$$β=180°-40°-40°=100°$$
Odpowiedź:
A. \(β=100°\)

