Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zaznaczając w układzie współrzędnych dane z treści zadania otrzymamy następującą sytuację:
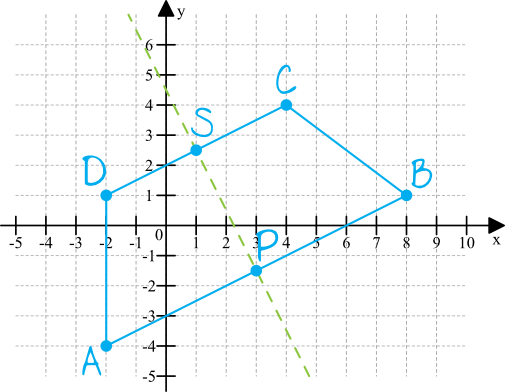
Krok 2. Wyznaczenie współrzędnych środka odcinka \(AB\).
Korzystając ze wzoru na środek odcinka i podstawiając odpowiednie współrzędne punktów \(A\) oraz \(B\) otrzymamy:
$$P=\left(\frac{x_{A}+x_{B}}{2};\frac{y_{A}+y_{B}}{2}\right) \\
P=\left(\frac{-2+8}{2};\frac{-4+1}{2}\right) \\
P=\left(\frac{6}{2};\frac{-3}{2}\right) \\
P=\left(3;-\frac{3}{2}\right)$$
Krok 3. Wyznaczenie współczynnika kierunkowego prostej \(AB\).
Oś symetrii jest prostą prostopadłą do prostej \(AB\), która przechodzi przez środek tego odcinka. Możemy wyznaczyć równanie prostej \(AB\) (np. metodą układu równań), ale nam tak naprawdę wystarczy poznanie współczynnika kierunkowego prostej \(AB\), a ten jesteśmy w stanie policzyć z prostego wzoru:
$$a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}} \\
a=\frac{1-(-4)}{8-(-2)} \\
a=\frac{1+4}{8+2} \\
a=\frac{5}{10} \\
a=\frac{1}{2}$$
Krok 4. Wyznaczenie równania prostej będącej osią symetrii trapezu.
Wiemy już, że oś symetrii trapezu jest prostą prostopadłą do prostej \(AB\), która przechodzi przez punkt \(P\). Aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych \(a\) musi być równy \(-1\). Skoro prosta \(AB\) ma współczynnik \(a=\frac{1}{2}\), to oś symetrii będzie mieć współczynnik \(a=-2\), bo \(-2\cdot\frac{1}{2}=-1\).
To oznacza, że oś symetrii da się opisać równaniem \(y=-2x+b\). Musimy jeszcze wyznaczyć wartość współczynnika \(b\), a dokonamy tego podstawiając do tego równania współrzędne punktu \(P=\left(3;-\frac{3}{2}\right)\), przez które ta prosta przechodzi. Otrzymamy w ten sposób:
$$y=-2x+b \\
-\frac{3}{2}=-2\cdot3+b \\
-\frac{3}{2}=-6+b \\
b=4\frac{1}{2}$$
Znając współczynnik \(b\) znamy już równanie naszej osi symetrii, a będzie to \(y=-2x+4\frac{1}{2}\).
Krok 5. Wyznaczenie współczynnika kierunkowego prostej \(CD\).
Prosta \(CD\) jest równoległa do prostej \(AB\), zatem te dwie proste będą miały identyczny współczynnik kierunkowy \(a\). Możemy więc już w tym momencie zapisać, że prosta \(CD\) ma współczynnik \(a=\frac{1}{2}\).
Krok 6. Wyznaczenie równania prostej \(CD\).
Wiemy już, że prosta \(CD\) ma współczynnik \(a=\frac{1}{2}\), czyli możemy ją opisać równaniem \(y=\frac{1}{2}x+b\). Brakujący współczynnik \(b\) poznamy podstawiając współrzędne jednego punktu przez które ta prosta przechodzi, czyli punktu \(C=(4,4)\). Otrzymamy wtedy:
$$y=\frac{1}{2}x+b \\
4=\frac{1}{2}\cdot4+b \\
4=2+b \\
b=2$$
W związku z tym prosta \(CD\) wyraża się równaniem \(y=\frac{1}{2}x+2\).
Krok 7. Wyznaczenie współrzędnych punktu \(S\).
Punkt \(S\) jest środkiem odcinka \(CD\) i jednocześnie jest miejscem przecięcia się osi symetrii oraz prostej \(CD\). Znamy równania jednej i drugiej prostej, zatem możemy ułożyć układ równań którego rozwiązaniem będą właśnie współrzędne punktu \(S\):
$$\begin{cases}
y=-2x+4\frac{1}{2} \\
y=\frac{1}{2}x+2
\end{cases}$$
Korzystając z metody podstawiania otrzymamy:
$$-2x+4\frac{1}{2}=\frac{1}{2}x+2 \\
-2\frac{1}{2}x=-2\frac{1}{2} \\
x=1$$
Znamy już współrzędną iksową, więc jeszcze musimy obliczyć współrzędną igrekową, a poznamy ją podstawiając \(x=1\) do dowolnego równania (np. pierwszego):
$$y=-2x+4\frac{1}{2} \\
y=-2\cdot1+4\frac{1}{2} \\
y=-2+4\frac{1}{2} \\
y=2\frac{1}{2}$$
To oznacza, że \(S=\left(1;2\frac{1}{2}\right)\).