Prawdopodobieństwo - zadania (egzamin ósmoklasisty)
Zadanie 1. (1pkt) Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
W pięciu rzutach standardową sześcienną kostką do gry, jeżeli wynik każdego rzutu będzie inny, można otrzymać łącznie dokładnie \(20\) oczek.
W \(16\) rzutach standardową sześcienną kostką do gry można otrzymać łącznie ponad \(100\) oczek.
Odpowiedź
1) PRAWDA
2) FAŁSZ
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
To zdanie jest prawdą. Gdybyśmy rzucali kostką sześciokrotnie i za każdym razem wynik rzutu byłby inny to otrzymalibyśmy sumę:
$$1+2+3+4+5+6=21$$
Skoro rzucamy pięciokrotnie, to widzimy wyraźnie, że wystarczy się pozbyć jedynki i otrzymamy dokładnie \(20\) oczek:
$$2+3+4+5+6=20$$
Krok 2. Ocena prawdziwości drugiego zdania.
Maksymalnie możemy wyrzucić szóstkę. Nawet jak \(16\) razy wyrzucimy tę szóstkę to otrzymamy łącznie:
$$16\cdot6=96\text{ oczek}$$
Zdanie jest więc nieprawdą.
Zadanie 3. (1pkt) Z cyfr \(2\), \(3\) i \(5\) Ania utworzyła wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Które z poniższych zdań jest prawdziwe?
Wyjaśnienie:
Krok 1. Zapisanie wszystkich liczb trzycyfrowych.
Z cyfr \(2\), \(3\) i \(5\) możemy utworzyć następujące liczby:
$$235, 253, 325, 352, 523, 532$$
Krok 2. Weryfikacja każdej z odpowiedzi.
Prześledźmy teraz każdą z odpowiedzi:
Odp. A. Wszystkie liczby utworzone przez Anię są nieparzyste
Komentarz: To nieprawda, bo tylko dwie liczby są parzyste.
Odp. B. Wszystkie liczby utworzone przez Anię są mniejsze od \(530\)
Komentarz: To nieprawda, bo liczba \(532\) jest większa od \(530\).
Odp. C. Dwie liczby utworzone przez Anię są podzielne przez \(5\).
Komentarz: To prawda, dwie liczby a mianowicie \(235\) oraz \(325\) są podzielne przez \(5\).
Odp. D. Wśród liczb utworzonych przez Anię są liczby podzielne przez \(3\)
Komentarz: To nieprawda, bo suma cyfr każdej z liczb jest równa \(10\), czyli liczby te nie są podzielne przez \(3\).
Zadanie 4. (1pkt) Rzucamy raz symetryczną sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że w rzucie tą kostką wypadnie liczba oczek większa od \(2\), ale mniejsza od \(6\)?
Wyjaśnienie:
Krok 1. Obliczenie liczby wszystkich możliwych wyników rzutu kostką (czyli zdarzeń elementarnych).
Rzucamy jedną sześcienną kostką, czyli możemy otrzymać jeden z sześciu wyników: \(1,2,3,4,5,6\). To oznacza, że mamy sześć różnych możliwości otrzymania wyniku, czyli \(|Ω|=6\).
Krok 2. Obliczenie liczby zdarzeń sprzyjających.
Sprzyjającym zdarzeniem jest wyrzucenie liczby większej od \(2\) i jednocześnie mniejszej od \(6\). Warunki naszego zadania spełniają zatem liczby: \(3,4,5\).
Interesują nas zatem trzy wyniki, czyli \(|A|=3\).
Krok 3. Obliczenie prawdopodobieństwa.
$$P(A)=\frac{|A|}{|Ω|}=\frac{3}{6}=\frac{1}{2}$$
Zadanie 5. (1pkt) Rzucamy jeden raz sześcienną kostką do gry. Oznaczmy przez \(p_{2}\) prawdopodobieństwo wyrzucenia liczby podzielnej przez \(2\), a przez \(p_{3}\) - prawdopodobieństwo wyrzucenia liczby podzielnej przez \(3\).
Oceń prawdziwość podanych zdań.
Liczba \(p_{2}\) jest mniejsza od liczby \(p_{3}\).
Liczby \(p_{2}\) i \(p_{3}\) są mniejsze od \(\frac{1}{6}\).
Odpowiedź
1) FAŁSZ
2) FAŁSZ
Wyjaśnienie:
Krok 1. Obliczenie prawdopodobieństwa wyrzucenia liczby podzielnej przez \(2\) oraz przez \(3\).
Na kostce możemy wylosować jedną z sześciu liczb: \(1, 2, 3, 4, 5, 6\).
Podzielne przez \(2\) są: \(2, 4, 6\)
Podzielne przez \(3\) są: \(3, 6\)
Prawd. wyrzucenia liczby podzielnej przez \(2\): \(p_{2}=\frac{3}{6}=\frac{1}{2}\)
Prawd. wyrzucenia liczby podzielnej przez \(3\): \(p_{3}=\frac{2}{6}=\frac{1}{3}\)
Krok 2. Ocena prawdziwości pierwszego zdania.
Pierwsze zdanie jest więc fałszem, bo \(\frac{1}{2}\gt\frac{1}{3}\).
Krok 3. Ocena prawdziwości drugiego zdania.
Drugie zdanie jest fałszywe, bo zarówno \(p_{2}=\frac{1}{2}\) jak i \(p_{3}=\frac{1}{3}\) są większe od \(\frac{1}{6}\).
Zadanie 6. (1pkt) Na rysunku przedstawiono siatkę nietypowej sześciennej kostki do gry. Rzucamy jeden raz taką kostką.
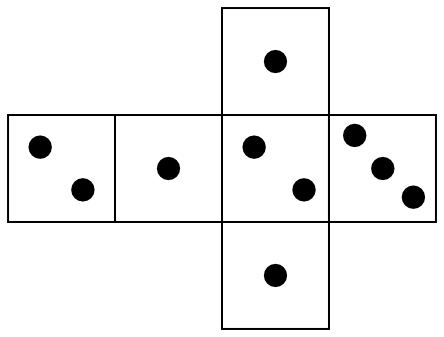
Oceń prawdziwość podanych zdań.
Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest \(2\) razy większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek.
Prawdopodobieństwo wyrzucenia liczby oczek mniejszej od \(3\) jest równe \(\frac{5}{6}\).
Odpowiedź
1) PRAWDA
2) PRAWDA
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Pierwsze zdanie jest prawdą, a wynika to z tego, że ścianek z liczbami nieparzystymi mamy dwa razy więcej niż tych z liczbami parzystymi (są cztery nieparzyste cyfry oraz dwie parzyste). To właśnie sprawia, że prawdopodobieństwo wyrzucenia liczby nieparzystej jest dwukrotnie większe.
Krok 2. Ocena prawdziwości drugiego zdania.
Drugie zdanie jest prawdą. Pięć z sześciu ścianek daje nam wynik mniejszy od \(3\), zatem prawdopodobieństwo wyrzucenia wyniku mniejszego od \(3\) jest równe \(\frac{5}{6}\).
Zadanie 8. (1pkt) Organizatorzy konkursu matematycznego przygotowali zestaw, w którym było \(10\) pytań z algebry i \(8\) pytań z geometrii. Uczestnicy konkursu losowali kolejno po jednym pytaniu, które po wylosowaniu było usuwane z zestawu. Pierwszy uczestnik wylosował pytanie z algebry.
Oceń prawdziwość podanych zdań.
Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z algebry jest równe \(\frac{9}{17}\).
Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z geometrii się nie zmieniło.
Odpowiedź
1) PRAWDA
2) FAŁSZ
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Pierwsze zdanie jest prawdą. Na początku mieliśmy \(18\) pytań w tym \(10\) z algebry. Jeżeli ktoś wylosował jedno pytanie z algebry, to tych pytań zostało \(17\) z czego z algebry jest \(9\). To oznacza, że faktycznie szanse na wylosowanie pytania z algebry wynoszą \(\frac{9}{17}\).
Krok 2. Ocena prawdziwości drugiego zdania.
Drugie zdanie jest nieprawdą. Na początku mieliśmy \(18\) pytań z czego \(8\) było z geometrii. Na początku szanse na wylosowanie zadania z geometrii wynosiły zatem \(\frac{8}{18}\). Po wylosowaniu pytania z algebry mamy w puli nadal \(8\) zadań z geometrii, ale wszystkich zadań jest już tylko \(17\), co sprawia że szanse na wylosowanie pytania z geometrii wynoszą teraz \(\frac{8}{17}\).
Zadanie 9. (1pkt) Do dwóch koszy wrzucono piłki szare i czarne. Na diagramie przedstawiono liczbę piłek każdego koloru w I i w II koszu.
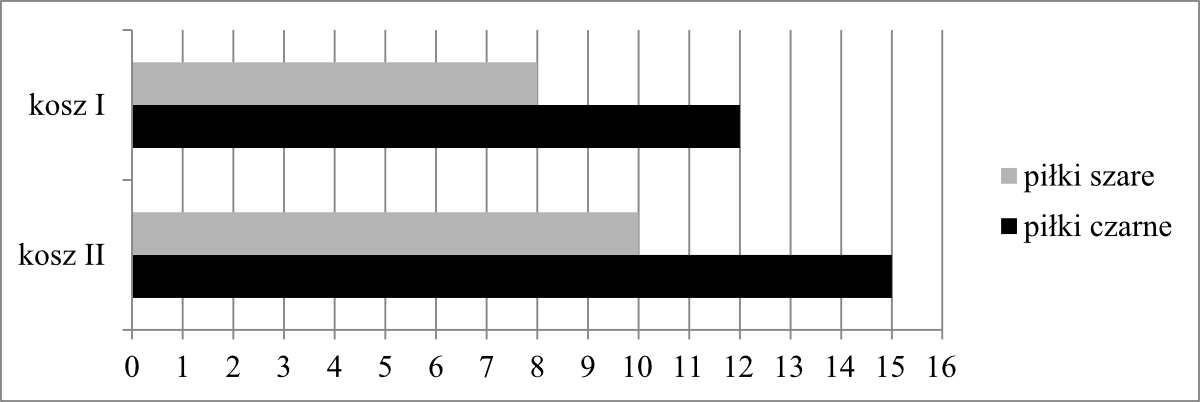
Czy wylosowanie piłki czarnej z kosza II jest bardziej prawdopodobne niż wylosowanie piłki czarnej z kosza I?
w koszu II jest więcej piłek czarnych niż w koszu I
stosunek liczby piłek czarnych do liczby wszystkich piłek jest taki sam w obu koszach
w koszu II jest o \(3\) piłki czarne więcej niż w koszu I, ale szarych - tylko o \(2\) więcej
Wyjaśnienie:
W pierwszym koszu znajduje się \(8+12=20\) piłek.
Skoro \(12\) z nich jest czarnych to szanse na wylosowanie czarnej piłki wynoszą \(\frac{12}{20}=\frac{3}{5}\).
W drugim koszu znajduje się \(10+15=25\) piłek.
Skoro \(15\) z nich jest czarnych to szanse na wylosowanie czarnej piłki wynoszą \(\frac{15}{25}=\frac{3}{5}\).
Szanse na wylosowanie czarnej piłki są więc takie same w obu koszach. Prawidłową odpowiedzią jest zatem: Nie, ponieważ stosunek liczby piłek czarnych do liczby wszystkich piłek jest taki sam w obu koszach.
Zadanie 10. (1pkt) W pudełku są \(2\) kule zielone, \(2\) białe i \(4\) czarne. Losujemy z pudełka \(1\) kulę. Czy prawdziwe jest stwierdzenie, że prawdopodobieństwo wylosowania kuli czarnej jest równe \(\frac{1}{2}\)?
w pudełku jest \(2\) razy mniej kul białych niż czarnych
w pudełku jest o połowę mniej kul zielonych niż kul czarnych
kule czarne stanowią połowę wszystkich kul w pudełku
Wyjaśnienie:
Krok 1. Obliczenie liczby wszystkich kul.
W pudełku znajduje się:
$$2+2+4=8\text{ kul}$$
Krok 2. Obliczenie prawdopodobieństwa wylosowania czarnej kuli.
Skoro czarnych kul są \(4\) sztuki, a w pudełku znajduje się tych kul \(8\), to szanse wylosowania czarnej kuli są równe \(\frac{4}{8}=\frac{1}{2}\).
Prawidłową odpowiedzią jest zatem: Tak, ponieważ kule czarne stanowią połowę wszystkich kul w pudełku.
Zadanie 11. (1pkt) Do gry planszowej używane są dwa bączki o kształtach przedstawionych na rysunkach. Każdy bączek po zatrzymaniu na jednym boku wielokąta wskazuje liczbę umieszczoną na jego tarczy. Na rysunku \(I\) bączek ma kształt pięciokąta foremnego z zaznaczonymi liczbami od \(1\) do \(5\). Na rysunku \(II\) bączek ma kształt sześciokąta foremnego z zaznaczonymi liczbami od \(1\) do \(6\).
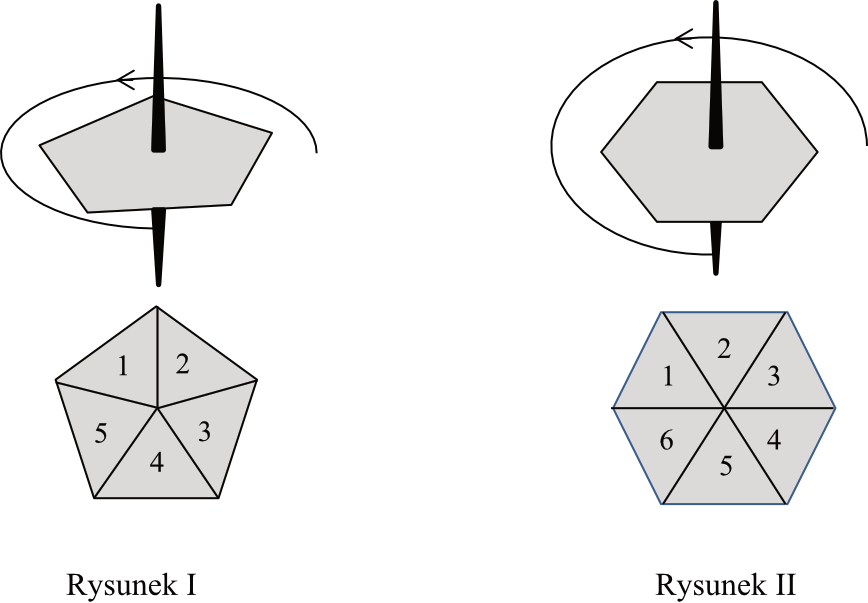
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Prawdopodobieństwo otrzymania liczby większej niż \(3\) na bączku z rysunku \(I\) jest większe niż \(\frac{1}{2}\).
Uzyskanie nieparzystej liczby na bączku z rysunku \(I\) jest tak samo prawdopodobne, jak uzyskanie nieparzystej liczby na bączku z rysunku \(II\).
Odpowiedź
1) FAŁSZ
2) FAŁSZ
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Na pierwszym bączku mamy pięć różnych liczb: \(1,2,3,4,5\). Nas interesuje wylosowanie liczby większej niż \(3\), czyli interesują nas dwa wyniki: \(4\) oraz \(5\). Skoro interesują nas dwa wyniki z pięciu możliwych, to prawdopodobieństwo wylosowania liczby większej niż \(3\) jest równe \(\frac{2}{5}\). To oznacza, że to prawdopodobieństwo jest mniejsze niż \(\frac{1}{2}\), czyli pierwsze zdanie jest fałszem.
Krok 2. Ocena prawdziwości drugiego zdania.
Na pierwszym bączku mamy pięć liczb, a trzy z nich to liczby nieparzyste. W związku z tym prawdopodobieństwo wylosowania liczby nieparzystej jest równe \(\frac{3}{5}\).
Na drugim bączku mamy sześć liczb, a trzy z nich to liczby nieparzyste. W związku z tym prawdopodobieństwo wylosowania liczby nieparzystej jest równe \(\frac{3}{6}=\frac{1}{2}\).
To oznacza, że prawdopodobieństwa są różne, czyli drugie zdanie jest fałszem.
Zadanie 12. (2pkt) Jedenaście piłeczek, ponumerowanych kolejnymi liczbami naturalnymi od \(1\) do \(11\), wrzucono do pudełka. Janek, nie patrząc na piłeczki, wyjmuje je z pudełka. Ile najmniej piłeczek musi wyjąć Janek, aby mieć pewność, że przynajmniej jedna wyjęta piłeczka jest oznaczona liczbą parzystą? Odpowiedź uzasadnij.
Odpowiedź
Janek musi wyjąć przynajmniej \(7\) piłeczek.
Wyjaśnienie:
Krok 1. Ustalenie liczby parzystych i nieparzystych piłeczek.
Liczb parzystych będzie łącznie pięć: \(2,4,6,8,10\)
Liczb nieparzystych będzie łącznie sześć: \(1,3,5,7,9,11\)
Krok 2. Wyznaczenie liczby piłeczek potrzebnych do wyciągnięcia.
Naszym zadaniem jest wylosowanie piłki z liczbą parzystą. W najgorszym możliwym wariancie Janek będzie losował od samego początku liczby nieparzyste. Aby mieć więc pewność, że wylosowana liczba jest parzysta, musimy wylosować przynajmniej \(7\) piłeczek, bo nawet jak sześć pierwszych liczb to będą numery nieparzyste, to siódmy będzie musiał już być parzysty, bo tylko takie zostaną wtedy w puli.
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy podasz poprawną odpowiedź, ale jej w żaden sposób nie uzasadnisz.
ALBO
• Gdy zauważysz, że można najpierw wyjmować wszystkie piłki z nieparzystymi numerami.
2 pkt
• Gdy otrzymasz oczekiwany wynik i go uzasadnisz.
Zadanie 14. (1pkt) W pudełku było \(20\) kul białych i \(10\) czarnych. Dołożono jeszcze \(10\) kul białych i \(15\) czarnych.
Oceń prawdziwość podanych zdań.
Przed dołożeniem kul prawdopodobieństwo wylosowania kuli białej było trzy razy większe niż prawdopodobieństwo wylosowania kuli czarnej.
Po dołożeniu kul prawdopodobieństwo wylosowania kuli czarnej jest większe niż prawdopodobieństwo wylosowania kuli białej.
Odpowiedź
1) FAŁSZ
2) FAŁSZ
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Pierwsze zdanie jest nieprawdą. Przed dołożeniem mieliśmy \(20+10=30\) kul. To sprawiało, że na początku prawdopodobieństwo wylosowania białej kuli wynosiło \(\frac{20}{30}=\frac{2}{3}\), a czarnej \(\frac{10}{30}=\frac{1}{3}\). Z tego wynika, że prawdopodobieństwo wylosowania kuli białej było na początku dwa razy większe, a nie trzy razy większe.
Krok 2. Ocena prawdziwości drugiego zdania.
Drugie zdanie jest nieprawdą. Wynika to chociażby z tego, że po dołożeniu mamy \(30\) kul białych i tylko \(25\) kul czarnych, więc nawet bez liczenia prawdopodobieństwa widać, że skoro czarnych kul jest mniej, to wylosowanie jednej z nich jest po prostu mniejsze niż w przypadku kuli białej.
Zadanie 15. (1pkt) Na festyn przygotowano loterię, w której było \(120\) losów, w tym \(80\) wygrywających. Przed rozpoczęciem festynu dołożono jeszcze \(20\) losów wygrywających i \(20\) przegrywających.
Czy prawdopodobieństwo wyciągnięcia losu wygrywającego w tej loterii zmieniło się po dołożeniu losów? Wybierz odpowiedź A albo B i jej uzasadnienie spośród 1., 2. albo 3.
różnica liczby losów wygrywających i przegrywających po dołożeniu losów jest taka sama jak na początku.
dołożono tyle samo losów wygrywających co przegrywających.
zmienił się stosunek liczby losów wygrywających do liczby wszystkich losów.
Wyjaśnienie:
Krok 1. Obliczenie prawdopodobieństwa przed dołożeniem losów.
Na początku mieliśmy \(120\) losów, w tym \(80\) wygrywających. Prawdopodobieństwo wygranej było więc równe \(\frac{80}{120}=\frac{2}{3}\).
Krok 2. Obliczenie prawdopodobieństwa po dołożeniu losów.
Po dołożeniu \(20\) losów wygrywających i \(20\) przegrywających mamy łącznie \(120+20+20=160\) losów. Losów wygrywających jest teraz \(80+20=100\). To oznacza, że prawdopodobieństwo wygranej wynosi teraz \(\frac{100}{160}=\frac{5}{8}\).
To oznacza, że prawdopodobieństwo wyciągnięcia losu wygrywającego się zmieniło, ponieważ zmienił się stosunek liczby losów wygrywających do liczby wszystkich losów.
a w 2 może być np. jeszcze 650
Ale to cyfra setek ma być o 6 mniejsza od cyfry jedności, a u Ciebie jest na odwrót :)
Uwielbiam prawdopodobieństwo! Czy nie mogą jedynie z tego działu testu zrobić? :) ;)
dokładnie
Zadania fajne, trochę trudniejsze od tych na egzaminie ósmoklasisty. Polecam!
Dzięki za objaśnienia!
bardzo przyjemne i łatwe zadania idealne na powtórzenie przed egzaminem
nieźle mi idzie :)
Bardzo fajne zadanka, polecam