Dany jest stożek o objętości \(8π\), w którym stosunek wysokości do promienia podstawy jest równy \(3:8\). Oblicz pole powierzchni bocznej tego stożka.
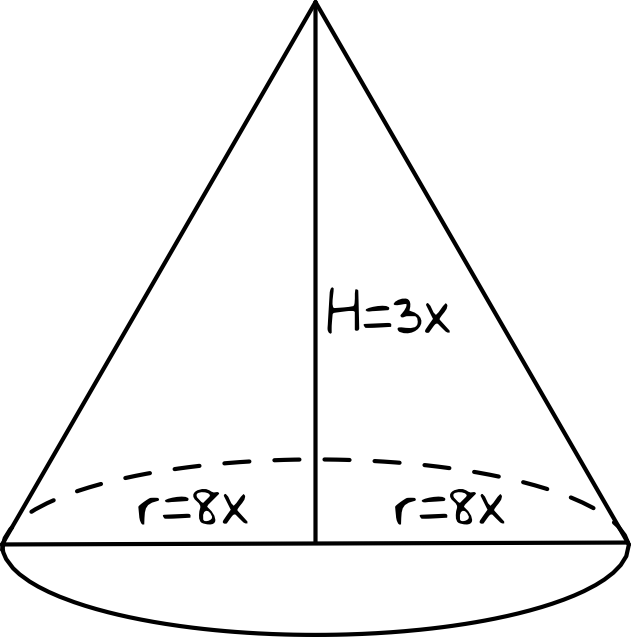
Oprócz naszkicowania sobie bryły wprowadźmy też oznaczenia, które pozwolą nam odnieść się do stosunku wysokości do promienia podstawy. Niech więc wysokość stożka będzie równa \(3x\), a promień podstawy \(8x\). Możemy też zapisać, że \(\frac{H}{r}=\frac{3}{8}\).
Skorzystamy tutaj ze wzoru na objętość stożka.
$$V=\frac{1}{3}πr^2\cdot H \\
8π=\frac{1}{3}π\cdot(8x)^2\cdot3x \\
8π=\frac{1}{3}π\cdot64x^2\cdot3x \\
8=64x^3 \\
x^3=\frac{1}{8} \\
x=\frac{1}{2}$$
To oznacza, że:
$$r=8x=8\cdot\frac{1}{2}=4 \\
H=3x=3\cdot\frac{1}{2}=\frac{3}{2}$$
Skorzystamy tutaj z Twierdzenia Pitagorasa:
$$r^2+H^2=l^2 \\
4^2+\left(\frac{3}{2}\right)^2=l^2 \\
16+\frac{9}{4}=l^2 \\
l^2=\frac{64}{4}+\frac{9}{4} \\
l^2=\frac{73}{4} \\
l=\sqrt{\frac{73}{4}} \\
l=\frac{\sqrt{73}}{2}$$
$$P_{b}=πrl \\
P_{b}=π\cdot4\cdot\frac{\sqrt{73}}{2} \\
P_{b}=2\sqrt{73}π$$
\(P_{b}=2\sqrt{73}π\)

