Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Na rysunku mamy deltoid, który możemy podzielić na dwa następujące trójkąty:
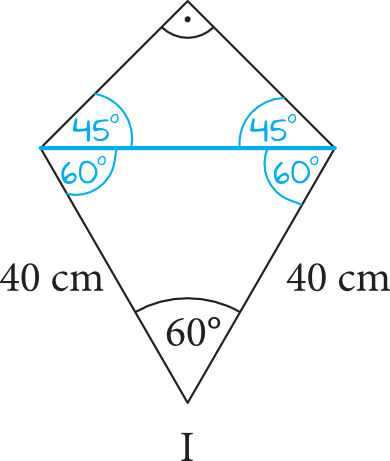
Na górze mamy trójkąt prostokątny o kątach \(45°, 45°, 90°\). Na dole powstał nam trójkąt równoboczny (możemy być pewni, że ten trójkąt jest równoboczny, bo kąt między ramionami o jednakowej długości ma miarę \(60°\), więc dwa kąty przy podstawie muszą mieć także po \(60°\)).
Krok 2. Obliczenie długości dwóch pozostałych ramion latawca.
Z własności trójkątów o kątach \(45°, 45°, 90°\) wynika, że gdy przyprostokątne mają długość \(a\), to przeciwprostokątna ma długość \(a\sqrt{2}\). W naszym przypadku przeciwprostokątna ma długość \(40cm\), zatem:
$$a\sqrt{2}=40 \\
a=\frac{40}{\sqrt{2}} \\
a=\frac{40\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
a=\frac{40\sqrt{2}}{2} \\
a=20\sqrt{2}$$
To oznacza, że górne ramiona latawca mają po \(20\sqrt{2}cm\).
Krok 3. Obliczenie obwodu latawca.
Zgodnie z obliczeniami, obwód latawca będzie równy:
$$Obw=2\cdot20\sqrt{2}+2\cdot40=40\sqrt{2}+80$$
Krok 4. Ustalenie, czy starczy taśmy.
Musimy jeszcze ustalić, czy \(1,5m\) taśmy wystarczy na oklejenie wszystkich krawędzi latawca. Mówiąc wprost, musimy ustalić, czy \(40\sqrt{2}cm+80cm\) to więcej, czy mniej niż \(1,5m\).
Wiedząc, że \(\sqrt{2}\approx1,41\) wyjdzie nam, że:
$$40\sqrt{2}+80\approx40\cdot1,41+80\approx56,4+80\approx136,4[cm]$$
To oznacza, że \(1,5m\) (czyli \(150cm\)) jak najbardziej wystarczy na oklejenie wszystkich krawędzi latawca.