Objętość ostrosłupa prawidłowego trójkątnego \(ABCS\) (tak jak na rysunku) jest równa \(72\), a promień okręgu wpisanego w podstawę \(ABC\) tego ostrosłupa jest równy \(2\). Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
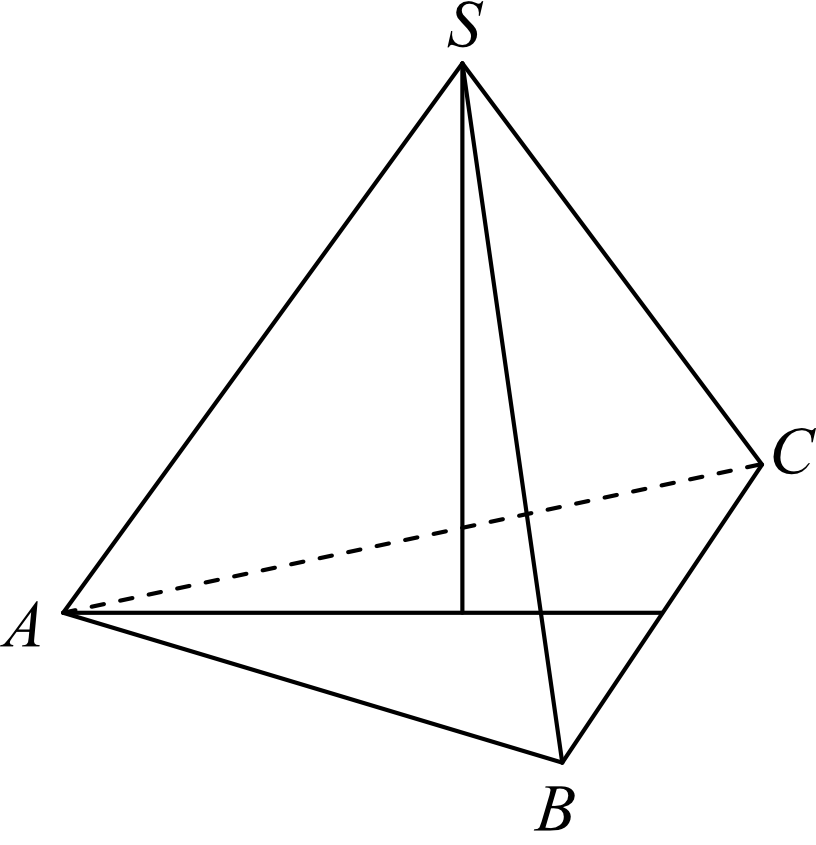
Dorysujmy sobie wysokość ściany bocznej, oznaczmy kąt którego tangensa musimy obliczyć. Przyjmijmy też, że krawędź podstawy jest równa \(a\):
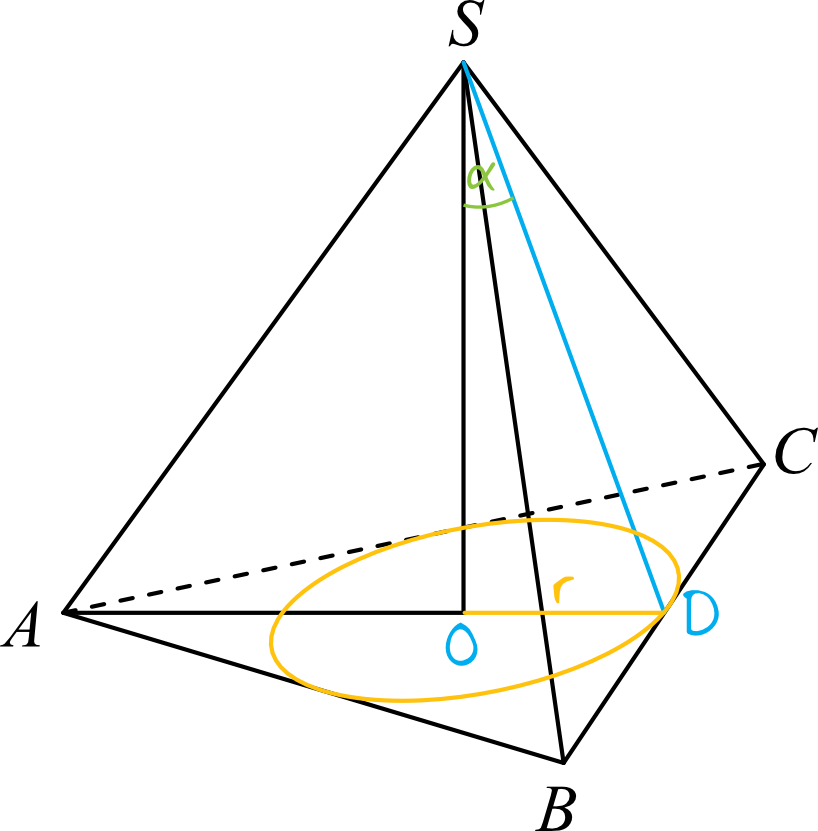
Musimy obliczyć tangens między wysokością ostrosłupa i jego ścianą boczną, czyli:
$$tgα=\frac{|OD|}{|SO|}$$
Długość odcinka \(OD\) jest nam znana, bo jest to długość promienia okręgu, czyli \(|OD|=r=2\). Potrzebujemy jeszcze wyznaczyć wysokość całego ostrosłupa i dopiero wtedy będziemy mogli obliczyć wartość tego tangensa.
Aby wyznaczyć wysokość ostrosłupa musimy najpierw policzyć pole podstawy, bowiem znając pole podstawy i objętość bryły (a ta jest podana w treści zadania) bez problemu obliczymy poszukiwaną wysokość ostrosłupa. Do obliczenia pola podstawy brakuje nam tak naprawdę znajomości długości krawędzi trójkąta równobocznego, który znajduje się w podstawie i to właśnie tą długość teraz wyznaczymy (wiemy, że jest to trójkąt równoboczny, bo jest to ostrosłup prawidłowy trójkątny).
Punktem wyjścia będzie promień okręgu wpisanego w podstawę (którego długość znamy, bo \(r=2\)), który stanowi \(\frac{1}{3}\) wysokości tego trójkąta. Skoro jest to trójkąt równoboczny to wzór na jego wysokość możemy zapisać jako \(h=\frac{a\sqrt{3}}{2}\), zatem:
$$r=\frac{1}{3}\cdot h\\
r=\frac{1}{3}\cdot\frac{a\sqrt{3}}{2} \\
2=\frac{a\sqrt{3}}{6} \\
a\sqrt{3}=12 \\
a=\frac{12}{\sqrt{3}}=\frac{12\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{12\sqrt{3}}{3}=4\sqrt{3}$$
Znając długość krawędzi możemy bez przeszkód obliczyć pole podstawy:
$$P_{p}=\frac{a^2\sqrt{3}}{4} \\
P_{p}=\frac{(4\sqrt{3})^2\sqrt{3}}{4} \\
P_{p}=\frac{16\cdot3\cdot\sqrt{3}}{4} \\
P_{p}=12\sqrt{3}$$
Zgodnie z tym co opisaliśmy sobie wcześniej – wysokość ostrosłupa wyznaczymy ze wzoru na objętość:
$$V=\frac{1}{3}P_{p}\cdot H \\
72=\frac{1}{3}\cdot12\sqrt{3}\cdot H \\
72=4\sqrt{3}\cdot H \\
H=\frac{72}{4\sqrt{3}} \\
H=\frac{18}{\sqrt{3}}=\frac{18\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{18\sqrt{3}}{3}=6\sqrt{3}$$
Znamy już wszystkie potrzebne miary, możemy więc wyznaczyć wartość tangensa między wysokością ostrosłupa i jego ścianą boczną:
$$|OD|=r=2 \\
|SO|=H=6\sqrt{3} \\
\text{więc} \\
tgα=\frac{|OD|}{|SO|} \\
tgα=\frac{2}{6\sqrt{3}}=\frac{2\cdot\sqrt{3}}{6\sqrt{3}\cdot\sqrt{3}}=\frac{2\sqrt{3}}{18}=\frac{\sqrt{3}}{9}$$
\(tgα=\frac{\sqrt{3}}{9}\)


A tg kąta alfa to nie będzie odcinek OS do odcinka OD?
Tangens to stosunek długości przyprostokątnej leżącej naprzeciwko kąta alfa względem przyprostokątnej leżącej przy tym kącie. Naprzeciwko kąta alfa jest OD, zatem to właśnie OD dzielimy przez SO :)
a co ze ścianą boczną? jak obliczyć jej wysokość i pole powierzchni?
W tym zadaniu nie trzeba jej obliczać ;) Ale jeśli chodzi Ci o jakiś podobny przykład to brakującą wysokość ściany bocznej obliczyć np. z twierdzenia Pitagorasa (zauważ, że na rysunku powstał specyficzny trójkąt prostokątny w którym dolna przyprostokątna to r, boczna przyprostokątna to H, no a przeciwprostokątna to będzie właśnie wysokość ściany bocznej) :)