Rozwiązanie
Krok 1. Obliczenie wartości \(f(0)\) oraz \(f(1)\).
Na początek obliczmy wartości \(f(0)\) oraz \(f(1)\), podstawiając odpowiednio do wzoru funkcji \(x=0\) oraz \(x=1\):
$$f(0)=(a+1)\cdot(0-2)^2\cdot(0+1) \\
f(0)=(a+1)\cdot(-2)^2\cdot1 \\
f(0)=(a+1)\cdot4\cdot1 \\
f(0)=4a+4$$
$$f(1)=(a+1)\cdot(1-2)^2\cdot(1+1) \\
f(1)=(a+1)\cdot(-1)^2\cdot2 \\
f(1)=(a+1)\cdot1\cdot2 \\
f(1)=2a+2$$
Krok 2. Podstawienie obliczonych wartości \(f(0)\) oraz \(f(1)\) do nierówności.
Podstawmy teraz to co przed chwilą wyznaczyliśmy do wskazanej nierówności:
$$f(0)\cdot f(1)\le16 \\
(4a+4)\cdot(2a+2)\le16 \\
8a^2+8a+8a+8\le16 \\
8a^2+16a+8\le16 \\
8a^2+16a-8\le0 \quad\bigg/:2 \\
a^2+2a-1\le0$$
Krok 3. Rozwiązanie powstałej nierówności kwadratowej.
Powstała nam klasyczna nierówność kwadratowa, której rozwiązywanie zaczniemy od wyznaczenia miejsc zerowych.
Współczynniki: \(a=1,\;b=2,\;c=-1\)
$$Δ=b^2-4ac=2^2-4\cdot1\cdot(-1)=4-(-4)=4+4=8 \\
\sqrt{Δ}=\sqrt{8}=2\sqrt{2}$$
$$a_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-2-2\sqrt{2}}{2\cdot1}=\frac{-2-2\sqrt{2}}{2}=-1-\sqrt{2} \\
a_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-2+2\sqrt{2}}{2\cdot1}=\frac{-2+2\sqrt{2}}{2}=-1+\sqrt{2}$$
Teraz musimy naszkicować naszą parabolę, zatem nanosimy wyznaczone przed chwilą miejsca zerowe (kropki muszą być zamalowane, bo w nierówności wystąpił znak \(\le\)) i rysujemy parabolę z ramionami skierowanymi do góry, bo współczynnik \(a\) jest dodatni:
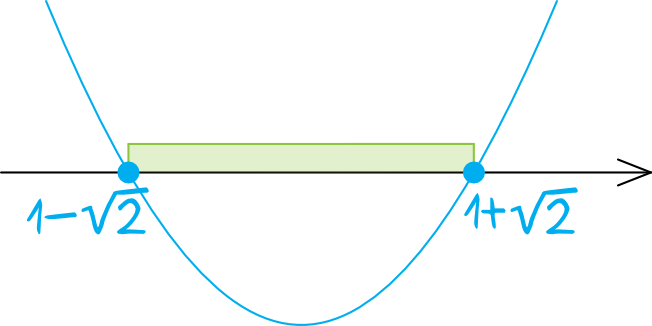
Z rysunku możemy teraz odczytać, że wartości mniejsze od zera są przyjmowane dla \(a\in\langle-1-\sqrt{2};-1+\sqrt{2}\rangle\).