Styczna do okręgu i okręgi styczne - zadania
Zadanie 14. (2pkt) Dany jest okrąg o środku w punkcie \(O\). Prosta \(KL\) jest styczna do tego okręgu w punkcie \(L\), a środek \(O\) tego okręgu leży na odcinku \(KM\) (zobacz rysunek). Udowodnij, że kąt \(KML\) ma miarę \(31°\).
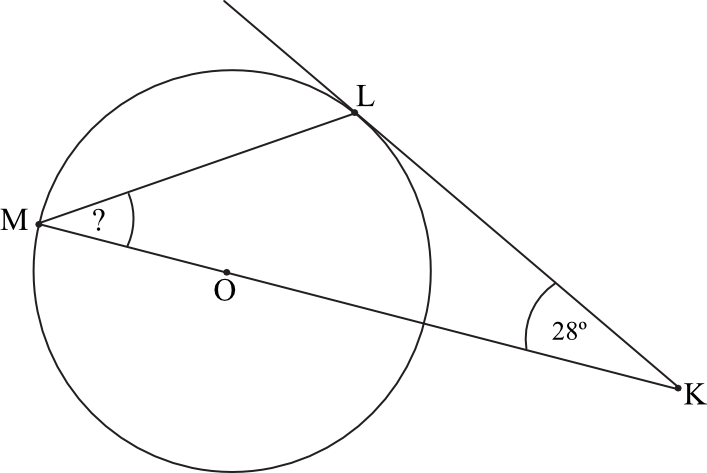
Odpowiedź
Udowodniono wykorzystując własności stycznej do okręgu.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Połączmy ze sobą punkty \(L\) oraz \(O\) (będzie to promień okręgu) i wprowadźmy sobie proste oznaczenia kątów:
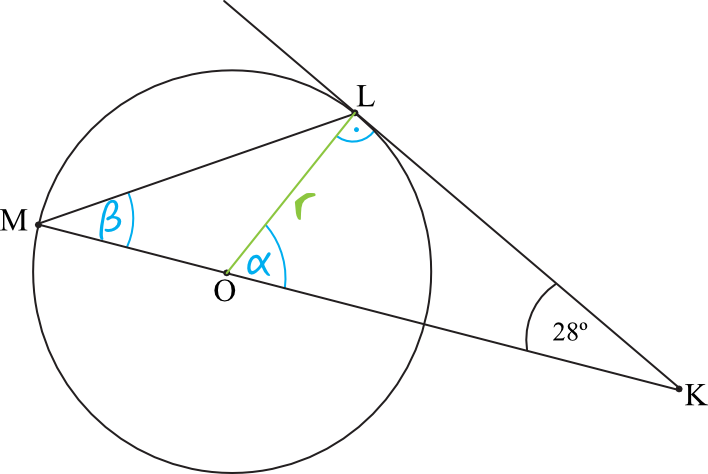
Z własności stycznych wiemy, że kąt między styczną, a promieniem okręgu, jest kątem prostym (patrz rysunek). To pozwoli nam w prosty sposób wyznaczyć miarę kąta \(α\).
Krok 2. Obliczenie miary kąta \(α\).
Skoro suma kątów w trójkącie \(OKL\) ma być równa \(180°\), to kąt \(α\) ma miarę:
$$α=180°-90°-28°=62°$$
Krok 3. Obliczenie miary kąta \(β\).
Z własności kątów środkowych i wpisanych opartych na tym samym łuku wiemy, że kąt wpisany w okręg (a takim jest nasz kąt \(β\)) jest dwa razy mniejszy od kąta środkowego (a takim jest tutaj kąt \(α\)). Zatem:
$$β=62°:2=31°$$
I właśnie to należało udowodnić.
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zaznaczysz (może być na rysunku), że kąt \(KLO\) jest prosty oraz zapiszesz że \(|\sphericalangle LOK|=2\cdot|\sphericalangle LMO|\) (patrz: Krok 3.)
ALBO
• Gdy dostrzeżesz, że \(|\sphericalangle LMO|=|\sphericalangle MLO|\), bo jest to trójkąt równoramienny.
ALBO
• Gdy połączysz punkt \(P\) z punktem przecięcia się okręgu i odcinka \(OK\), oznaczysz ten punkt przykładowo jako \(N\) i zauważysz, że powstał trójkąt prostokątny, a z własności stycznych do okręgu zapiszesz, że \(|\sphericalangle NLK|=|\sphericalangle LMN|\)
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Zadanie 15. (2pkt) Dane są dwa okręgi o środkach w punktach \(P\) i \(R\), styczne zewnętrznie w punkcie \(C\). Prosta \(AB\) jest styczna do obu okręgów odpowiednio w punktach \(A\) i \(B\) oraz \(|\sphericalangle APC|=α\) i \(|\sphericalangle ABC|=β\) (zobacz rysunek). Wykaż, że \(α=180°-2β\).
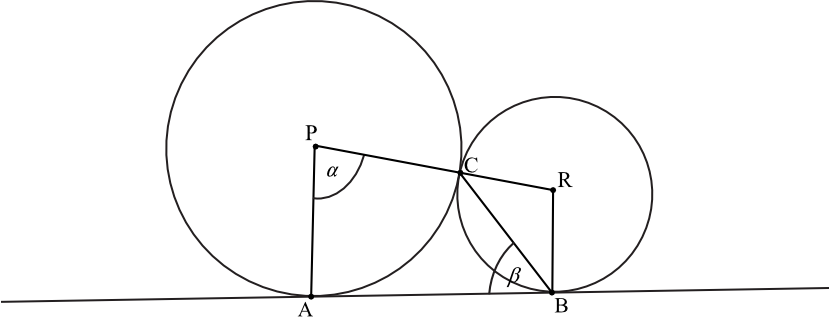
Odpowiedź
Udowodniono wykorzystując własności kątów.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Musimy dostrzec dwie bardzo ważne rzeczy.
Po pierwsze \(|\sphericalangle CBR|=|\sphericalangle BCR|\), bo trójkąt \(CRB\) jest równoramienny (ramiona mają długość promienia okręgu).
Po drugie \(|\sphericalangle PAB|=90°\) oraz \(|\sphericalangle ABR|=90°\), bo promienie okręgów poprowadzone do stycznej są do niej prostopadłe.
Spróbujmy więc nanieść na nasz rysunek te oznaczenia i jeszcze może dodatkowo zapiszmy, że \(|\sphericalangle PCB|=δ\) (przyda nam się to w kolejnym kroku):

Krok 2. Wyznaczenie miar kątów \(γ\) oraz \(δ\).
Skoro \(|\sphericalangle ABR|=90°\), to możemy napisać, że:
$$β+γ=90° \\
γ=90°-β$$
Kąt \(δ\) wyznaczymy z własności kątów przyległych:
$$|\sphericalangle PCB|+|\sphericalangle BCR|=180° \\
δ+γ=180°$$
Podstawiając wyznaczoną przed chwilą wartość \(γ=90°-β\) otrzymamy:
$$δ+90°-β=180° \\
δ=90°+β$$
Krok 3. Wyznaczenie miary kąta \(α\).
Patrzymy na czworokąt \(ABCP\). Suma miar tego czworokąta musi być równa \(360°\), zatem:
$$90°+β+δ+α=360° \\
90°+β+(90°+β)+α=360° \\
180°+2β+α=360° \\
α=180°-2β$$
Udało nam się wyznaczyć dokładnie taką samą wartość kąta \(α\) jak w treści zadania, więc dowód możemy uznać za skończony.
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wykorzystasz własności trójkątów równoramiennych i/lub stycznych do okręgu, zapiszesz (lub zaznaczysz na rysunku) poszczególne miary kątów powiązując je z kątami \(α\) oraz \(β\) (patrz: Krok 1 oraz 2.).
Uwaga: W zadaniu jest bardzo dużo dróg dojścia do uzasadnienia, możesz więc przyznać sobie 1 punkt także za zapisanie zupełnie innych relacji, byleby były one powiązane z kątami \(α\) oraz \(β\) i by prowadziły do ostatecznego rozwiązania.
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Zadanie 16. (2pkt) W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość \(10\) i jest styczna do wewnętrznego okręgu (zobacz rysunek).
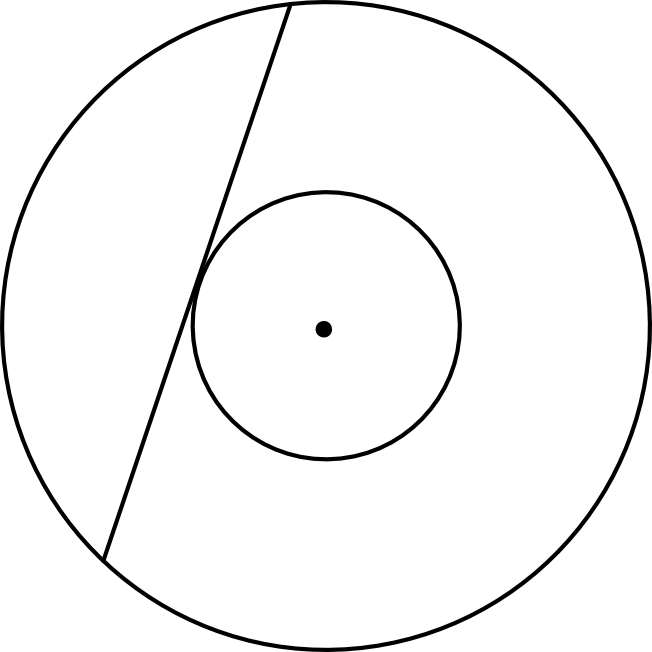
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
Odpowiedź
Udowodniono wykorzystując Twierdzenie Pitagorasa.
Wyjaśnienie:
Krok 1. Zapisanie wzoru na pole pierścienia.
Pole pierścienia możemy zapisać jako różnicę między polem powierzchni dużego koła (o promieniu duże \(R\)) i małego (o promieniu małe \(r\)), zatem:
$$P=πR^2-πr^2=π(R^2-r^2)$$
No i teraz naszym zadaniem jest doprowadzenie do sytuacji w której pozbędziemy się wartości promieni.
Krok 2. Sporządzenie rysunku poglądowego.
Wiedząc, że styczna jest zawsze prostopadła do promienia okręgu, możemy stworzyć następujący trójkąt prostokątny:
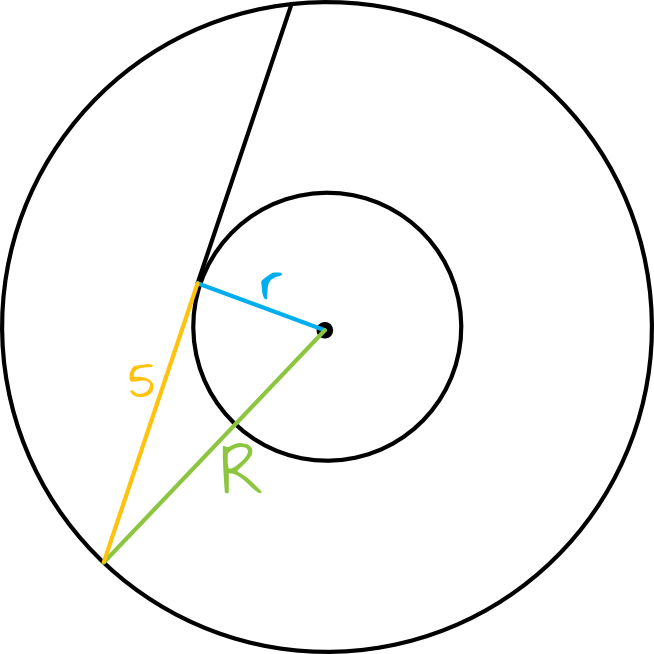
Krok 3. Wyznaczenie wartości wyrażenia \(R^2-r^2\) z Twierdzenia Pitagorasa.
Podstawiając do Twierdzenia Pitagorasa dane i oznaczenia z naszego rysunku otrzymamy:
$$r^2+5^2=R^2 \\
r^2+25=R^2 \\
25=R^2-r^2$$
Krok 4. Zakończenie dowodzenia.
Podstawiając wartość \(R^2-r^2\) do wzoru na pole pierścienia otrzymamy, że:
$$P=π(R^2-r^2) \\
P=25π$$
I taki zapis kończy nasze dowodzenie, bo udało nam się określić wzór na pole pierścienia bez występowania długości promieni.
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz wzór na pole pierścienia \(P=πR^2-πr^2\) (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Czy wzory z zadania jedenastego znajdę w tablicach matematycznych dostępnych na maturze?
Wzór na środek odcinka jak najbardziej jest w tablicach. Te rozpiski na xS oraz yS są tak naprawdę wzięte z tego głównego wzoru :)
Czy wzór (x−a)2+(y−b)2=r2 znajduje się w tablicach matematycznych na maturze?
Tak, nazywa się to „równanie okręgu” i jest na 6 stronie :)
które z tych zadań dotyczą obecnej matury?
A no właśnie, muszę chyba spisać dla Was te zadanka, które wypadają z matury 2021 ;)
Dlaczego w zadaniu 9 w rozwiązaniu jest nagle (x-(-4))? Skąd się to wzięło?
+4 zamieniłem na -(-4), bo w równaniu okręgu mamy (x-a)^2, czyli w nawiasie musimy mieć minusa :)
Zadanie 22, czy takie same bądź podobne może być na maturze w 2021 roku?
Takiego zadanka nie będzie, bo styczne do okręgu wypadły z matury 2021 ;)
Czemu połowa zadań została usunięta?
Ojj połowa to raczej nie, raptem kilka ;) Po prostu dostosowałem się lepiej do nowej matury :)
czy zależności w trójkącie równobocznym r=1/3h lub R=2/3h są w tablicach maturalnych?
Tak, są te zależności zapisane także w tablicach, choć prawdę mówiąc mógłby przy nich być lepszy rysunek (z lepszym objaśnieniem) :)
Czy wzór na obliczenie odległości między dwoma punktami (z zadania 12.) znajdę w tablicach matematycznych na maturze? Z góry dziękuję za odpowiedź :)
Tak! To standardowy wzór na długość odcinka w układzie współrzędnych :)
Super zadanka :)