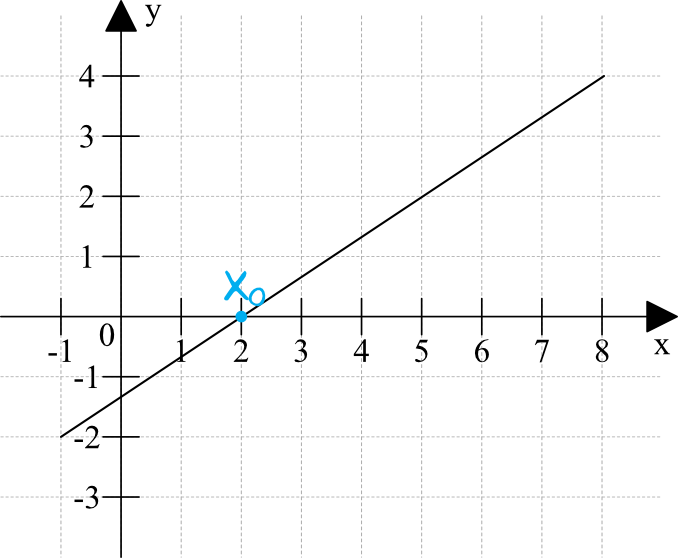
Miejsce zerowe funkcji to taki argument \(x\) dla którego funkcja przyjmuje wartość \(y=0\). Obrazowo rzecz ujmując będzie to miejsce przecięcia się wykresu funkcji z osią iksów, które bardzo często oznaczamy symbolem \(x_{o}\).
Bardzo często spotkamy się z zadaniami typu: „Wyznacz miejsca zerowe funkcji (i tu pada wzór funkcji)”. Jak takie zadania powinniśmy rozwiązywać? Spójrzmy na prosty przykład:
Chcemy wyznaczyć miejsce zerowe, czyli sprawdzić dla jakiego argumentu powyższa funkcja przyjmuje wartość równą \(0\). Możemy więc albo pod \(f(x)\) podstawić zero, otrzymując równanie \(0=2x+8\), albo też wytłumaczyć sobie to w ten sposób, że chcemy sprawdzić kiedy \(2x+8\) jest równe \(0\), dzięki czemu otrzymamy identyczne równanie \(2x+8=0\). To w jaki sposób będziemy sobie podchodzić do zadania jak widać nie ma większego znaczenia, bo otrzymaliśmy identyczne równania. W związku z tym:
$$2x+8=0 \\
2x=-8 \\
x=-4$$
Miejscem zerowym funkcji jest zatem \(x=-4\).
Cały czas postępujemy tak samo – musimy sprawdzić kiedy funkcja wyrażona wzorem \(\sqrt{2}-x\) będzie równa \(0\), zatem:
$$\sqrt{2}-x=0 \\
x=\sqrt{2}$$
Miejscem zerowym tej funkcji jest \(x=\sqrt{2}\).
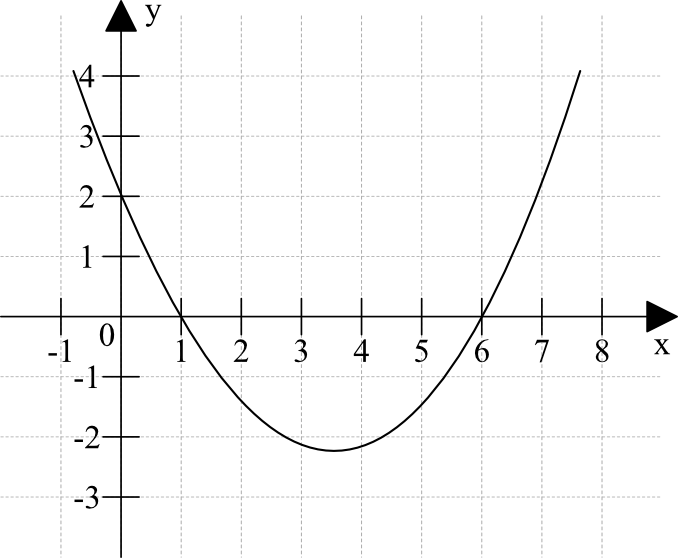
Miejsca zerowe to miejsca w których funkcja osiąga wartość równą zero, czyli są to miejsca przecięcia się wykresu z osią iksów. Powyższa funkcja ma więc dwa miejsca zerowe: \(x=1\) oraz \(x=6\).
Tym razem mamy funkcję kwadratową, ale cały czas tok postępowania jest taki sam – musimy sprawdzić kiedy \(2x^2+9x-18\) będzie równe \(0\).
$$2x^2+9x-18=0$$
To równanie kwadratowe najprościej będzie obliczyć tzw. metodą delty:
Współczynniki: \(a=2,\;b=9,\;c=-18\)
$$Δ=b^2-4ac=9^2-4\cdot2\cdot(-18)=81-(-144)=225 \\
\sqrt{Δ}=\sqrt{225}=15$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-9-15}{2\cdot2}=\frac{-24}{4}=-6 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-9+15}{2\cdot2}=\frac{6}{4}=1,5$$
Ta funkcja kwadratowa ma dwa miejsca zerowe: \(x=-6 \;\lor\; x=1,5\).
Tutaj mamy funkcję kwadratową, ale przedstawioną w postaci iloczynowej, czyli takiej z której bardzo łatwo jest odczytać miejsca zerowe. Tradycyjnie przyrównujemy \((x-2)(2x+3)\) do zera, otrzymując równanie:
$$(x-2)(2x+3)=0$$
Rozwiązywanie tego typu równań jest bardzo proste. Nie musimy wymnażać przez siebie nawiasów. Aby zaszła równość \((x-2)(2x+3)=0\) to któryś z nawiasów musi „wyzerować” nam to równanie, czyli albo wartość nawiasu \(x-2\) jest równa \(0\), albo \(2x+3\) jest równe \(0\). To znaczy, że:
$$x-2=0 \quad\lor\quad 2x+3=0 \\
x=2 \quad\lor\quad 2x=-3 \\
x=2 \quad\lor\quad x=-\frac{3}{2}$$
To oznacza, że ta funkcja kwadratowa ma dwa miejsca zerowe: \(x=2 \;\lor\; x=-\frac{3}{2}\).

dlaczego w ostatnim przykładzie jest wynik -1,5 zamiast -0,75??
Musimy rozwiązać równanie 2x+3=0, bo przyrównujemy wartości w nawiasach do zera. Rozwiązaniem tego równania jest x=-1,5, a nie -0,75 ;)
Bo -3/2 to -1 i 1/2 czyli -1,5