Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f. Drugim miejscem zerowym

Na rysunku przedstawiono fragment wykresu funkcji kwadratowej $f$. Jednym z miejsc zerowych tej funkcji jest liczba $2$. Do wykresu funkcji $f$ należy punkt $(0,3)$. Prosta o równaniu $x=-2$ jest osią symetrii paraboli, będącej wykresem funkcji $f$.

Drugim miejscem zerowym funkcji $f$ jest liczba:

A. $-2$

B. $-3$

C. $-4$

D. $-6$

Rozwiązanie

Z własności funkcji kwadratowych wiemy, że miejsca zerowe są oddalone od osi symetrii o jednakową liczbę jednostek. Znane nam miejsce zerowe $x=2$ jest oddalone od osi symetrii $x=-2$ o $4$ jednostki, wiec analogicznie poszukiwane miejsce zerowe także musi być o te $4$ jednostki oddalone:
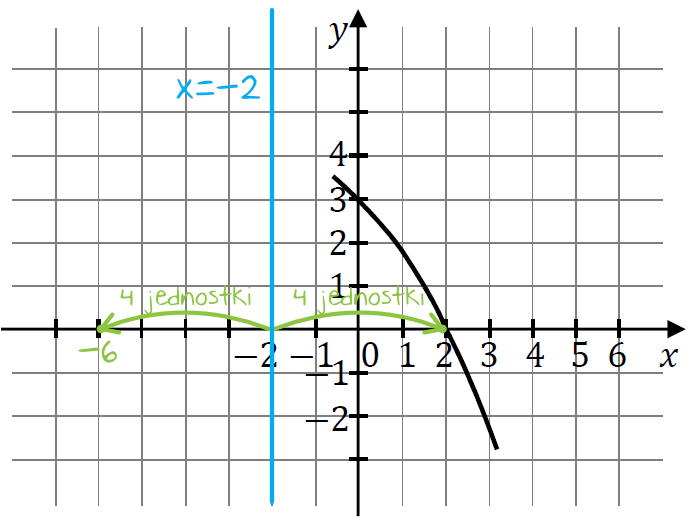
matura z matematyki

Oczywiście do tego samego wyniku możemy dojść w nieco bardziej matematyczny sposób, przy użyciu średniej arytmetycznej. Wiedząc, że oś symetrii znajduje się dokładnie między dwoma miejscami zerowymi, moglibyśmy zapisać, że:
$$\frac{x+2}{2}=-2 \\
x+2=-4 \\
x=-6$$

Odpowiedź