Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy sobie zwizualizować to zadanie. Narysujmy parabolę (jej ramiona będą skierowane do dołu, bo po wymnożeniu wszystkich wyrazów współczynnik kierunkowy \(a\) wyjdzie ujemny) i zobaczmy jak będzie wyglądać zbiór wartości funkcji. Z postaci iloczynowej możemy też szybko wyznaczyć miejsca zerowe tej funkcji, bo wystarczy przyrównać wartości w nawiasach do zera:
$$x+3=0 \quad\lor\quad x-4=0 \\
x=-3 \quad\lor\quad x=4$$
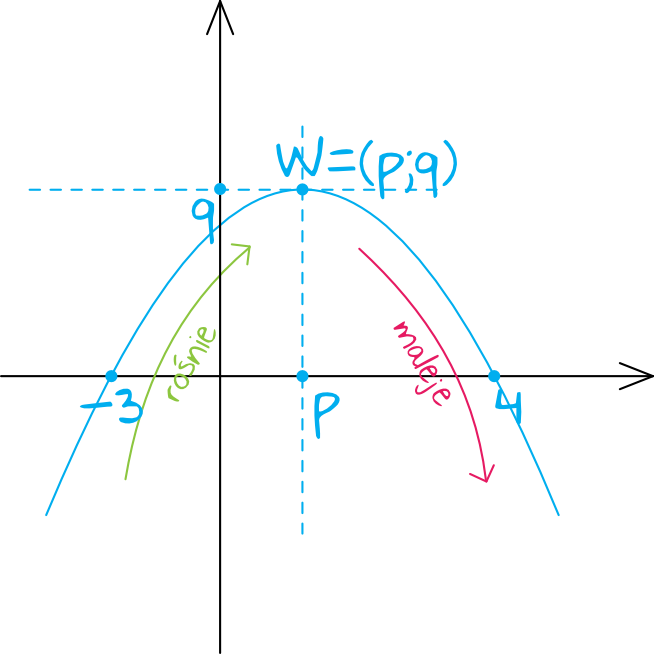
Zbiór wartości odczytujemy z osi igreków. Z rysunku wynika, że nasza funkcja przyjmuje wartości od minus nieskończoności do współrzędnej igrekowej wierzchołka tej paraboli (zapisywanej w matematyce symbolem \(q\)).
Krok 2. Zapisanie równania w postaci ogólnej.
Współrzędną \(q\) możemy obliczyć ze wzoru: \(q=\frac{-Δ}{4a}\). Musimy zatem obliczyć deltę, a żeby obliczyć deltę to najpierw całe równanie musimy zapisać w postaci ogólnej, zatem wymnażając wszystkie wyrazy otrzymamy:
$$f(x)=-2(x+3)(x-4) \\
f(x)=-2(x^2-4x+3x-12) \\
f(x)=-2(x^2-x-12) \\
f(x)=-2x^2+2x+24$$
Krok 3. Obliczenie współrzędnej \(q\).
Najpierw obliczmy potrzebną deltę:
Współczynniki: \(a=-2,\;b=2,\;c=24\)
$$Δ=b^2-4ac=2^2-4\cdot(-2)\cdot24=4-(-192)=196$$
W związku z tym współrzędna \(q\) będzie równa:
$$q=\frac{-Δ}{4a} \\
q=\frac{-196}{4\cdot(-2)} \\
q=\frac{-196}{-8} \\
q=24\frac{1}{2}$$
Krok 4. Ustalenie zbioru wartości funkcji.
Zgodnie z naszym szkicowym rysunkiem i obliczeniami możemy zapisać, że zbiorem wartości naszej funkcji jest przedział:
$$y\in(-\infty,q\rangle \\
y\in(-\infty,24\frac{1}{2}\rangle$$