Rozwiązanie
Krok 1. Obliczenie miejsc zerowych wielomianu.
Nierówność jest zapisana w postaci iloczynowej, czyli w bardzo łatwy sposób wyznaczymy jej miejsca zerowe - wystarczy przyrównać wartość każdego z nawiasów do zera:
$$x-1=0 \quad\lor\quad x+2=0 \\
x=1 \quad\lor\quad x=-2$$
Krok 2. Szkicowanie wykresu paraboli.
Ramiona paraboli będą skierowane do góry, bo gdybyśmy zaczęli wymnażać te nawiasy, to przed \(x^2\) nie stałby żaden minus. Zaznaczamy wyznaczone przed chwilą miejsca zerowe (kropki będą niezamalowane, bo w nierówności wystąpił znak \(\gt\)) i szkicujemy wykres paraboli.
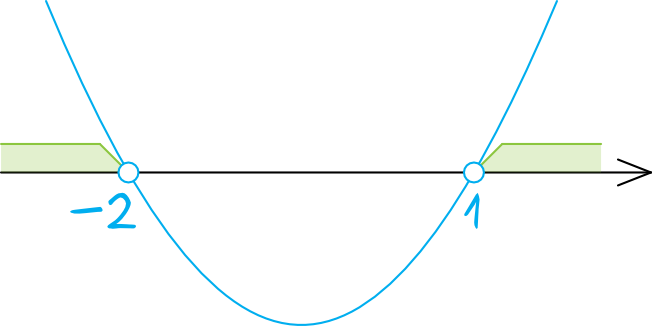
Krok 3. Odczytanie rozwiązania.
Szukamy wartości większych od zera, zatem rozwiązaniem naszej nierówności jest suma przedziałów: \(x\in(-\infty,-2)\cup(1,\infty)\).