Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować parabolę, której osią symetrii jest prosta o równaniu \(x=7\):
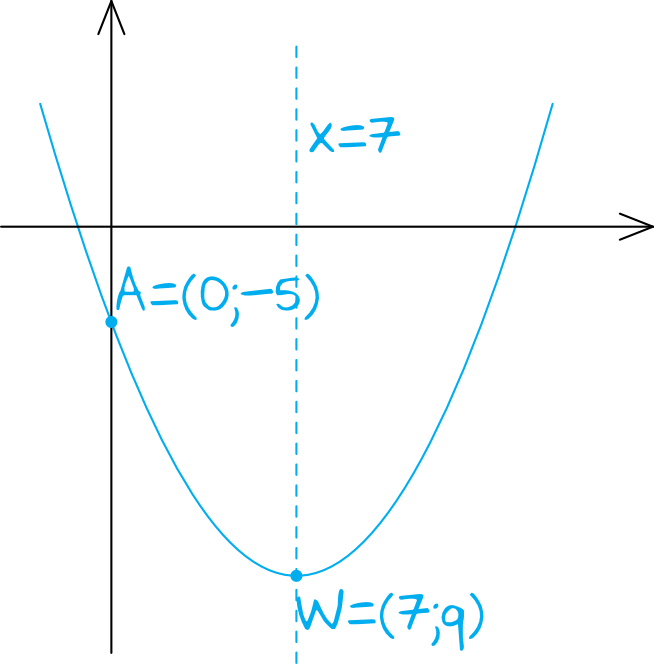
Z rysunku wynika, że skoro osią symetrii jest prosta \(x=7\), to musi ona przechodzić przez wierzchołek. To z kolei prowadzi nas do wniosku, że współrzędną iksową wierzchołka paraboli jest \(p=7\).
Krok 2. Obliczenie wartości współczynnika \(b\).
Współrzędną iksową wierzchołka obliczamy ze wzoru \(p=\frac{-b}{2a}\). Wartość współczynnika \(a\) jest znana i wynosi \(a=1\) (bo przed \(x^2\) nie ma żadnej liczby). W związku z tym jesteśmy w stanie obliczyć wartość współczynnika \(b\):
$$p=\frac{-b}{2a} \\
7=\frac{-b}{2\cdot1} \\
7=\frac{-b}{2} \\
14=-b \\
b=-14$$
Krok 3. Obliczenie wartości współczynnika \(c\).
Współczynnik \(c\) w postaci ogólnej mówi nam o tym w którym miejscu parabola przecina oś igreków. Przykładowo jak parabola przecina oś igreków w wartości \(y=4\), to współczynnik \(c=4\). Tak się składa, że punkt \(A\) jest właśnie miejscem przecięcia się paraboli z osią igreków (bo ma współrzędną iksową równą \(0\)). W związku z tym możemy zapisać, że \(c=-5\).
Jeżeli o tej własności nie pamiętamy, to do wzoru funkcji \(f(x)=x^2-14x+c\) wystarczy podstawić współrzędne punktu \(A\), czyli \(x=0\) oraz \(y=-5\). Otrzymamy wtedy:
$$f(x)=x^2-14x+c \\
-5=0^2-14\cdot0+c \\
-5=0+0+c \\
c=-5$$