W trapezie prostokątnym ABCD, w którym AB||CD i |AB|=2|CD|, poprowadzono przekątne AC i BD

W trapezie prostokątnym $ABCD$, w którym $AB||CD$ i $|AB|=2|CD|$, poprowadzono przekątne $AC$ i $BD$, przecinające się w punkcie $S$. Udowodnij, że odległość punktu $S$ od ramienia $AD$, prostopadłego do podstaw, jest trzy razy mniejsza niż długość podstawy $AB$.

Rozwiązanie

Krok 1. Dostrzeżenie podobieństwa trójkątów.
Spójrzmy na trójkąty $ABS$ oraz $CDS$. Są to trójkąty podobne i wiemy to na podstawie cechy kąt-kąt-kąt, co wynika wprost z własności kątów naprzemianległych oraz wierzchołkowych.
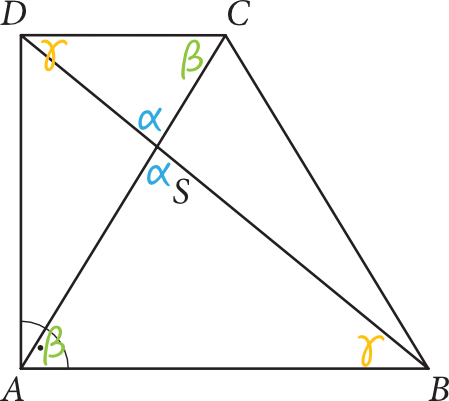
matura z matematyki

Krok 2. Obliczenie skali podobieństwa.
Jeżeli przyjmiemy, że trójkąt $CDS$ jest trójkątem podstawowym, a trójkąt $ABS$ trójkątem podobnym, to skala podobieństwa wyniesie:
$$k=\frac{|AB|}{|CD|}$$

Z treści zadania wynika, że $|AB|=2|CD|$, zatem:
$$k=\frac{2|CD|}{|CD|} \\
k=2$$

Uwaga: Gdybyśmy przyjęli, że trójkąt $ABS$ jest podstawowy, a trójkąt $CDS$ jest podobny, to skala podobieństwa będzie równa $k=\frac{1}{2}$ i jest to jak najbardziej poprawny tok rozwiązywania zadania. Różnica jest tylko taka, że w dalszych krokach trzeba konsekwentnie odnosić się do wybranej przez siebie figury podobnej.

Krok 3. Sporządzenie rysunku pomocniczego.
Zaznaczmy na rysunku poszukiwaną odległość punktu $S$ od ramienia $AD$ i zobaczmy co nam w tym momencie powstanie:
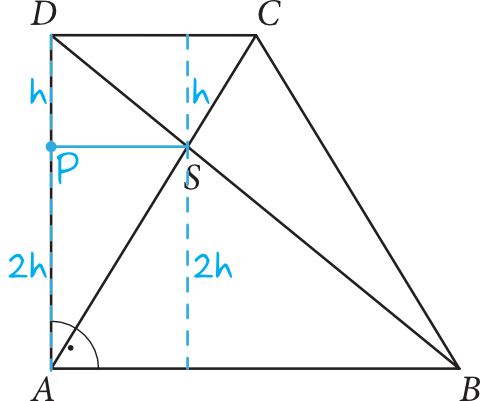
matura z matematyki

Tutaj kluczową obserwacją jest to, co wynika ze skali podobieństwa $k=2$. Jeżeli wysokość trójkąta $CDS$ ma długość $h$, to wysokość trójkąta $ABS$ będzie dwukrotnie dłuższa, czyli wyniesie $2h$. To z kolei prowadzi nas do wniosku, że odcinek $AD$ ma miarę równą $h+2h=3h$.

Krok 4. Dostrzeżenie podobieństwa trójkątów.
Spójrzmy teraz na trójkąty $ABD$ oraz $PSD$. Te trójkąty są także podobne (wynika to z cechy kąt-kąt-kąt, bowiem odcinek $PS$ jest równoległy do odcinka $AB$). Jeżeli więc odcinek $PD$ jest trzykrotnie krótszy od odcinka $AD$, to odcinek $PS$ będzie także trzykrotnie krótszy od odcinka $AB$.

Możemy to nawet zapisać matematycznie w formie proporcji. Jeżeli przyjmiemy, że trójkąt $ABD$ jest trójkątem podstawowym, a trójkąt $PSD$ jest trójkątem podobnym, to skala podobieństwa wyniesie:
$$k=\frac{|PD|}{|AD|} \\
k=\frac{h}{3h} \\
k=\frac{1}{3}$$

Z tego też względu każdy odcinek trójkąta podobnego $PSD$ jest trzykrotnie krótszy od odpowiadającemu mu odcinkowi trójkąta podstawowego $ABD$, zatem $|PS|=\frac{1}{3}|AB|$, co należało udowodnić.

Odpowiedź

Udowodniono korzystając z podobieństwa trójkątów.

Zadania

W trapezie prostokątnym ABCD, w którym AB||CD i |AB|=2|CD|, poprowadzono przekątne AC i BD

W trapezie prostokątnym \(ABCD\), w którym \(AB||CD\) i \(|AB|=2|CD|\), poprowadzono przekątne \(AC\) i \(BD\), przecinające się w punkcie \(S\). Udowodnij, że odległość punktu \(S\) od ramienia \(AD\), prostopadłego do podstaw, jest trzy razy mniejsza niż długość podstawy \(AB\).