Rozwiązanie
Krok 1. Obliczenie długości krawędzi podstawy.
Skoro jest to ostrosłup prawidłowy czworokątny to znaczy, że w jego podstawie znajduje się kwadrat. Wiemy, że kwadrat ten ma pole powierzchni równe \(100\), zatem:
$$P=a^2 \\
100=a^2 \\
a=10 \quad\lor\quad a=-10$$
Ujemny wynik oczywiście odrzucamy i zostaje nam, że krawędź boczna ma długość \(a=10\).
Krok 2. Obliczenie wysokości ściany bocznej.
W ścianie bocznej o polu powierzchni \(P_{b}=65\) mamy trójkąt o podstawie \(a=10\). To oznacza, że możemy bez przeszkód obliczyć wysokość ściany bocznej.
$$P_{b}=\frac{1}{2}ah \\
65=\frac{1}{2}\cdot10\cdot h \\
65=5h \\
h=13$$
Krok 3. Sporządzenie rysunku pomocniczego.
Spróbujmy teraz narysować ten ostrosłup i zaznaczyć w nim obliczone przed chwilą wielkości:
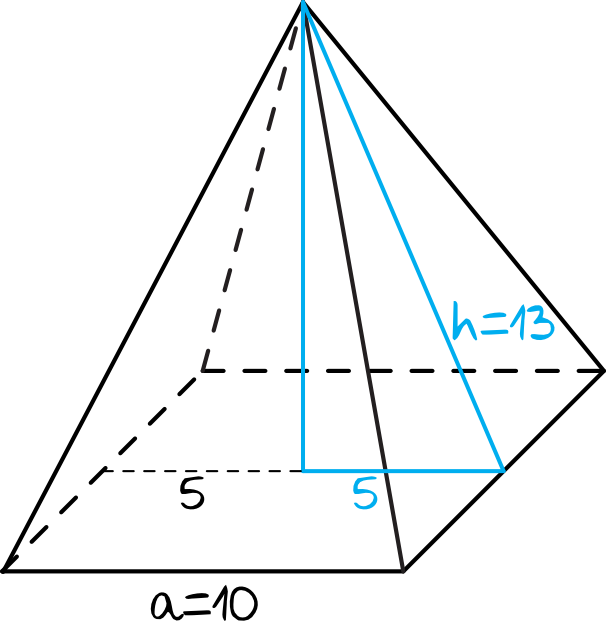
Z rysunku wynika, że wysokość ostrosłupa (potrzebna do obliczenia objętości) będziemy mogli wyznaczyć z trójkąta prostokątnego, którego dolna przyprostokątna jest połową boku kwadratu (stąd też bierze się długość równa \(5\)), a przeciwprostokątna ma długość \(13\).
Krok 4. Obliczenie wysokości ostrosłupa.
Wysokość tego ostrosłupa najprościej będzie wyznaczyć z Twierdzenia Pitagorasa:
$$5^2+H^2=13^2 \\
25+H^2=169 \\
H^2=144 \\
H=12 \quad\lor\quad H=-12$$
Ujemną wartość odrzucamy, bo wysokość nie może być ujemna, zatem \(H=12\).
Krok 5. Obliczenie objętości ostrosłupa.
Znając pole podstawy oraz wysokość ostrosłupa możemy bez przeszkód obliczyć objętość bryły:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot100\cdot12 \\
V=400$$