Wysokość trójkąta to najkrótszy odcinek łączący bok trójkąta z przeciwległym wierzchołkiem. To oznacza, że wysokość pada zawsze pod kątem prostym (w przeciwnym wypadku nie byłby to najkrótszy bok). Na matematyce wysokość trójkąta (oraz innych figur) oznaczamy literą \(h\).

Warto też pamiętać, że w każdym trójkącie jesteśmy w stanie wyznaczyć trzy wysokości – w zależności od tego na który bok ta wysokość jest opuszczona:
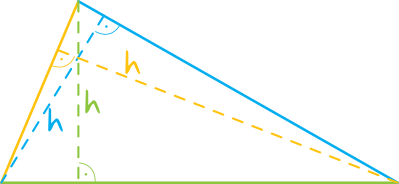
Powyższa uwaga jest o tyle istotna, że rozwiązując zadania musimy zwracać uwagę na to jaka wysokość nas interesuje, tym bardziej że zazwyczaj wszystkie te wysokości mają różne długości.
Wzór na wysokość trójkąta
Jeżeli przekształcimy wzór na pole trójkąta \(P=\frac{1}{2}ah\) to otrzymamy podstawowy wzór na wysokość trójkąta:
$$P=\frac{1}{2}ah \quad\bigg/\cdot2 \\
2P=ah \quad\bigg/:a \\
h=\frac{2P}{a}$$
W związku z tym jeżeli znamy pole powierzchni trójkąta i znamy długość boku na który pada wysokość, to bez problemu jesteśmy w stanie wyznaczyć wysokość. Nie musimy się tego wzoru uczyć na pamięć, bo zawsze kiedy zajdzie taka potrzeba będziemy mogli przekształcić odpowiednie działanie.
W starszych klasach ważnym zagadnieniem są charakterystyczne własności wysokości, które występują w bardzo charakterystycznych trójkątach takich jak trójkąt równoboczny, równoramienny oraz prostokątny.
Wysokość trójkąta równobocznego
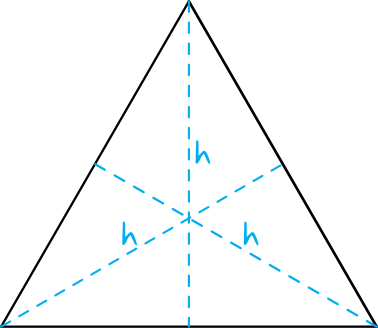
Z wysokościami trójkąta równobocznego związane są cztery bardzo charakterystyczne własności:
· Wszystkie trzy wysokości trójkąta są jednakowej długości
· Wysokości trójkąta równobocznego pokrywają się z dwusiecznymi kątów i symetralnymi boków
· Miejsce przecięcia się trzech wysokości jest jednocześnie środkiem okręgu wpisanego i opisanego na trójkącie
· Wysokość trójkąta równobocznego możemy obliczyć korzystając ze specjalnego wzoru: \(h=\frac{a\sqrt{3}}{2}\)
Wysokość trójkąta równoramiennego
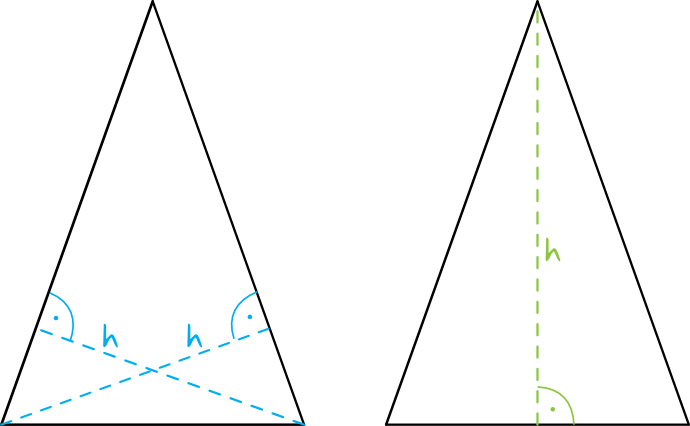
Wysokości trójkąta równoramiennego mają następujące własności:
· Dwie z trzech wysokości będą miały tą samą długość (to będą te wysokości, które są opuszczone na ramiona trójkąta).
· Trzecia wysokość trójkąta równoramiennego jest jednocześnie linią, która dzieli taki trójkąt na dwa przystające prostokątne trójkąty. Tym samym dzieli ona podstawę trójkąta na dwie równe części.
Wysokość trójkąta prostokątnego
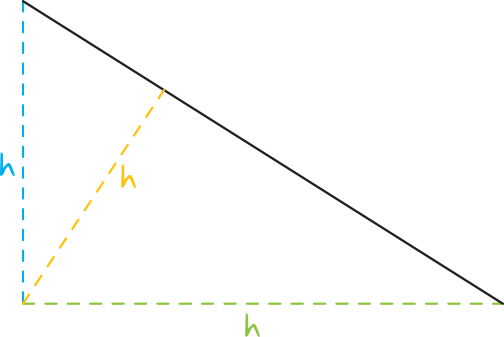
O wysokościach w trójkącie prostokątnym możemy powiedzieć, że:
· Miejscem przecięcia się trzech wysokości trójkąta jest wierzchołek kąta prostego
· Dwie wysokości pokrywają się z przyprostokątnymi trójkąta (znając więc długości przyprostokątnych znamy jednocześnie wysokość trójkąta).
Spójrzmy teraz na przykładowe zadania w których przydadzą nam się poznane przed chwilą informacje.
Do takich zadań bardzo często podchodzimy w ten sposób, że po prostu zapisujemy sobie wzór na pole trójkąta i podstawiamy odpowiednie liczby, rozwiązując tym samym równanie z jedną niewiadomą:
$$P=\frac{1}{2}ah \\
20=\frac{1}{2}\cdot10\cdot h \\
20=5h \\
h=4[cm]$$
W ten oto sposób obliczyliśmy, że wysokość trójkąta jest równa \(h=4cm\).
Skorzystamy tutaj ze wzoru \(h=\frac{a\sqrt{3}}{2}\) do którego wystarczy tylko podstawić \(a=6cm\). W związku z tym:
$$h=\frac{a\sqrt{3}}{2} \\
h=\frac{6\sqrt{3}}{2} \\
h=3\sqrt{3}[cm]$$
Z treści zadania wiemy, że jest to trójkąt prostokątny, zatem jedna z przyprostokątnych będzie podstawą, a druga będzie wysokością trójkąta (nie ma znaczenia czy zapiszemy \(a=6\) oraz \(h=8\), czy też \(a=8\) oraz \(h=6\)). W związku z tym:
$$P=\frac{1}{2}ah \\
P=\frac{1}{2}\cdot6\cdot8 \\
P=3\cdot8 \\
P=24[cm^2]$$

h=(ab)/c
Świetne!
super! teraz już wszystko rozumiem