Tworząca stożka ma długość \(4\) i jest nachylona do płaszczyzny podstawy pod kątem \(45°\). Wysokość tego stożka jest równa:
\(2\sqrt{2}\)
\(16π\)
\(4\sqrt{2}\)
\(8π\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
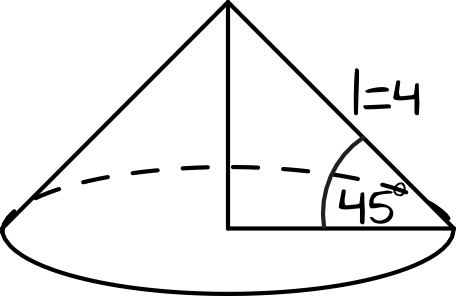
Widzimy, że promień, wysokość oraz tworząca stożka utworzyły nam trójkąt prostokątny \(ABC\). Znamy tylko długość tworzącej stożka oraz miarę kąta jej nachylenia do podstawy, więc chcąc obliczyć wysokość stożka musimy skorzystać albo z własności trójkątów \(45°, 45°, 90°\) albo z trygonometrii.
Krok 2. Obliczenie wysokości stożka.
Korzystając z zasad trygonometrii otrzymamy:
$$sin45°=\frac{h}{l} \\
\frac{\sqrt{2}}{2}=\frac{h}{4} \\
h=2\sqrt{2}$$
Odpowiedź:
A. \(2\sqrt{2}\)

