Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować całą tę sytuację, zaznaczając przy okazji środek odcinka \(AB\):
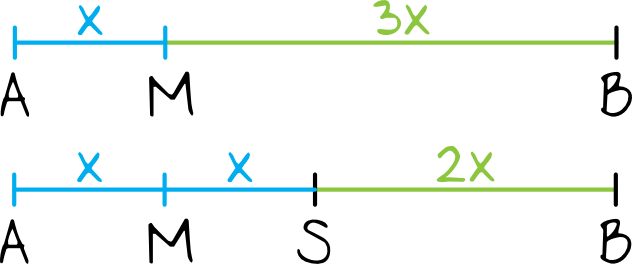
Okazuje się, że punkt M jest tak naprawdę środkiem odcinka \(AS\). Musimy zatem najpierw wyznaczyć współrzędne punktu \(S\) (który jest środkiem odcinka \(AB\)), a następnie przejdziemy do wyznaczenia współrzędnych punktu \(M\).
Krok 2. Obliczenie współrzędnych punktu \(S\).
Środek odcinka \(AB\) o współrzędnych \(A=(x_{A};y_{A})\) oraz \(B=(x_{B};y_{B})\) możemy opisać wzorem:
$$S=\left(\frac{x_{A}+x_{B}}{2};\frac{y_{A}+y_{B}}{2}\right)$$
Dla przejrzystości zapisu obliczmy każdą ze współrzędnych oddzielnie:
$$x_{S}=\frac{x_{A}+x_{B}}{2} \\
x_{S}=\frac{-23+17}{2} \\
x_{S}=\frac{-6}{2} \\
x_{S}=-3 \\
\quad \\
y_{S}=\frac{y_{A}+y_{B}}{2} \\
y_{S}=\frac{-9+21}{2} \\
y_{S}=\frac{12}{2} \\
y_{S}=6$$
To oznacza, że \(S=(-3;6)\).
Krok 3. Obliczenie współrzędnych punktu \(M\).
Zgodnie z analizą rysunku pomocniczego, punkt \(M\) jest środkiem odcinka \(AS\), zatem korzystając z tych samych wzorów co w drugim kroku możemy zapisać, że:
$$x_{M}=\frac{x_{A}+x_{S}}{2} \\
x_{M}=\frac{-23-3}{2} \\
x_{M}=\frac{-26}{2} \\
x_{M}=-13 \\
\quad \\
y_{M}=\frac{y_{A}+y_{S}}{2} \\
y_{M}=\frac{-9+6}{2} \\
y_{M}=\frac{-3}{2} \\
y_{M}=-\frac{3}{2}$$
To oznacza, że \(M=\left(-13;-\frac{3}{2}\right)\).
Krok 4. Obliczenie iloczynu współrzędnych punktu \(M\).
Na koniec zgodnie z poleceniem musimy podać wartość iloczynu obydwu współrzędnych punktu \(M\), zatem:
$$-13\cdot\left(-\frac{3}{2}\right)=\frac{39}{2}=19,5$$