Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
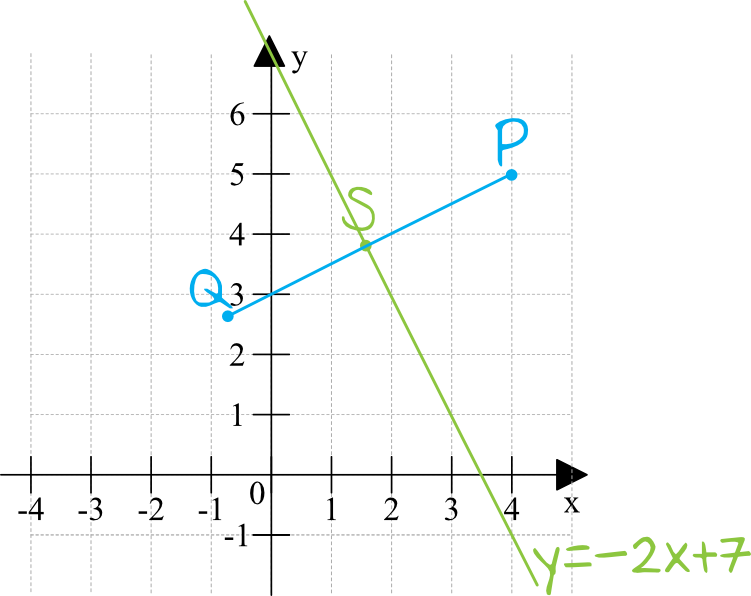
Krok 2. Wyznaczenie wartości współczynnika \(a\) prostej \(PQ\).
Symetralna jest prostą prostopadłą, która przechodzi przez środek odcinka. Z własności prostych prostopadłych wiemy, że aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). Skoro więc nasza pierwsza prosta ma współczynnik \(a=-2\), to prosta przechodząca przez odcinek \(PQ\) (możemy ją nawet roboczo nazwać prostą \(PQ\)) będzie mieć współczynnik \(a=\frac{1}{2}\), bo \(-2\cdot\frac{1}{2}=-1\).
Krok 3. Wyznaczenie równania prostej \(PQ\).
Wiemy już, że współczynnik \(a\) prostej \(PQ\) jest równy \(a=\frac{1}{2}\), czyli że prosta \(PQ\) wyraża się równaniem \(y=\frac{1}{2}x+b\). Wiemy też, że prosta ta przechodzi przez punkt \(P=(4;5)\), zatem podstawiając \(x=4\) oraz \(y=5\) poznamy brakujący współczynnik \(b\):
$$5=\frac{1}{2}\cdot4+b \\
5=2+b \\
b=3$$
To oznacza, że prosta \(PQ\) wyraża się równaniem \(y=\frac{1}{2}x+3\).
Krok 4. Wyznaczenie współrzędnych punktu przecięcia się prostych.
Skoro znamy równanie prostej \(PQ\) i znamy równanie symetralnej, to możemy obliczyć miejsce przecięcia się tych prostych, czyli współrzędne środka odcinka \(PQ\). Z geometrycznej interpretacji układu równań wiemy, że rozwiązaniem układu równań dwóch prostych są współrzędne przecięcia się tych prostych, zatem:
\begin{cases}
y=-2x+7 \\
y=\frac{1}{2}x+3
\end{cases}
Korzystając z metody podstawiania otrzymamy:
$$-2x+7=\frac{1}{2}x+3 \\
2\frac{1}{2}x=4 \\
x=1,6$$
Podstawiając wyznaczoną przed chwilą wartość \(x=1,6\) do dowolnego z równań z układu (np. pierwszego) otrzymamy:
$$y=-2\cdot(1,6)+7 \\
y=3,8$$
To oznacza, że środek odcinka \(PQ\) znajduje się w punkcie \(S=(1,6; 3,8)\).
Krok 5. Obliczenie współrzędnych punktu \(Q\).
Znamy współrzędne punktu \(P\) oraz środka \(S\), stąd też możemy bez przeszkód wyznaczyć współrzędne punktu \(Q\). Dla przejrzystości obliczeń dobrze jest obliczyć sobie oddzielnie współrzędną iksową i igrekową punktu \(Q\):
$$x_{S}=\frac{x_{P}+x_{Q}}{2} \\
1,6=\frac{4+x_{Q}}{2} \\
3,2=4+x_{Q} \\
x_{Q}=-0,8 \\
\quad \\
y_{S}=\frac{y_{P}+y_{Q}}{2} \\
3,8=\frac{5+y_{Q}}{2} \\
7,6=5+y_{Q} \\
y_{Q}=2,6$$
To oznacza, że \(Q=(-0,8; 2,6)\) lub jak kto woli \(Q=\left(-\frac{4}{5};\frac{13}{5}\right)\).