Punkty \(A\), \(B\) i \(C\) leżą na okręgu o środku \(O\) (zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy \(AOB\) ma miarę:
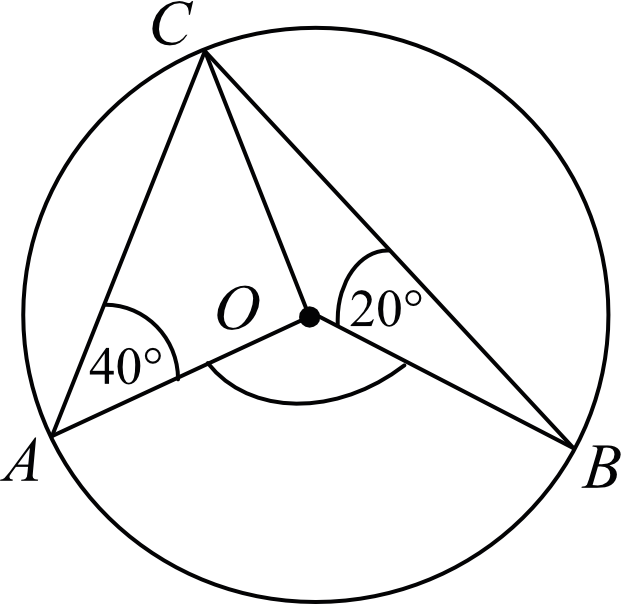
Spójrzmy najpierw na trójkąt \(AOC\). Na pewno jest to trójkąt równoramienny, którego ramiona \(AO\) oraz \(CO\) mają długość równą długości promienia okręgu. To oznacza, że podstawą tego trójkąta jest bok \(AC\). Wiemy z własności trójkątów równoramiennych, że kąty przy podstawie mają tą samą miarę. W związku z tym:
$$|\sphericalangle ACO|=|\sphericalangle OAC|=40°$$
Analogicznie będzie wyglądać sytuacja w tym węższym trójkącie \(BOC\). Tutaj także jest to trójkąt równoramienny i także jego kąty przy podstawie mają równą długość, zatem:
$$|\sphericalangle BCO|=|\sphericalangle OBC|=20°$$
Miara kąta \(ACB\) jest sumą miar dwóch kątów, które wyznaczyliśmy sobie przed chwilą:
$$|\sphericalangle ACB|=|\sphericalangle ACO|+|\sphericalangle BCO| \\
|\sphericalangle ACB|=40°+20° \\
|\sphericalangle ACB|=60°$$
Z własności kątów środkowych i wpisanych wiemy, że jeśli te dwa kąty są opisane na tym samym łuku (a tak jest w naszym przypadku), to miara kąta środkowego jest dwa razy większa od miary kąta wpisanego. Więc:
$$|\sphericalangle AOB|=60°\cdot2 \\
|\sphericalangle AOB|=120°$$
C. \(120°\)

