Okręgi o środkach S1=(3,4) oraz S2=(9,-4) i równych promieniach są styczne zewnętrznie

Okręgi o środkach \(S_{1}=(3,4)\) oraz \(S_{2}=(9,-4)\) i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy:

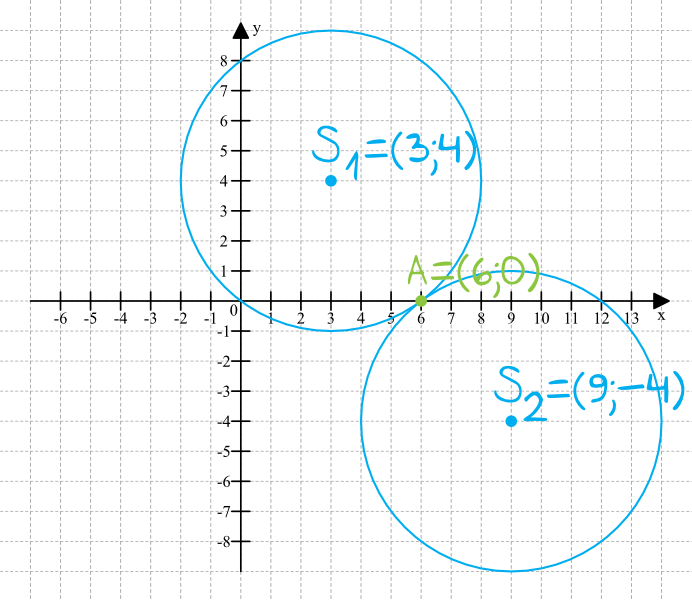
Jeśli dość dokładnie narysujemy ten szkic to tak naprawdę już z samego rysunku będziemy w stanie odczytać długość promienia, zwłaszcza że punkt styczności wypadnie w równym punkcie \(A=(6;0)\). Skąd wiemy, że akurat w tym punkcie wypadnie punkt styczności? Skoro promienie mają być sobie równe, to punkt styczności będzie tak naprawdę środkiem odcinka \(S_{1}S_{2}\) (możemy go wyznaczyć albo matematycznie, albo nawet linijką jeśli inaczej nie potrafimy).

To jest jednak taki alternatywny sposób (gdybyśmy nie umieli tego obliczyć nieco bardziej matematycznie). My natomiast spróbujmy policzyć to zadanie z wykorzystaniem wzoru na odległość między dwoma punktami.

Zgodnie ze wzorem na odległość między dwoma punktami mamy:
$$|S_{1}S_{2}|=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2} \\
|S_{1}S_{2}|=\sqrt{(9-3)^2+(-4-4)^2} \\
|S_{1}S_{2}|=\sqrt{6^2+(-8)^2} \\
|S_{1}S_{2}|=\sqrt{36+64} \\
|S_{1}S_{2}|=\sqrt{100} \\
|S_{1}S_{2}|=10$$

Z rysunku bardzo wyraźnie wynika, że odległość między środkami \(S_{1}\) oraz \(S_{2}\) jest równa sumie długości promieni. W treści zadania mamy informację, że długości tych promieni są równe, więc oznaczając każdy z nich jako \(r\) otrzymamy:
$$r+r=10 \\
2r=10 \\
r=5$$

C. \(5\)