Rozwiązanie
Krok 1. Wyznaczenie miejsc zerowych funkcji kwadratowej.
Funkcja zapisana jest w postaci iloczynowej, zatem bez problemu możemy wyznaczyć jej miejsca zerowe. W tym celu wystarczy przyrównać wartości w nawiasach do zera:
$$x+1=0 \quad\lor\quad x-3=0 \\
x=-1 \quad\lor\quad x=3$$
Krok 2. Sporządzenie rysunku pomocniczego.
Funkcja ma współczynnik kierunkowy \(a=-2\) (czyli ujemny), zatem nasza parabola będzie wyglądać następująco:
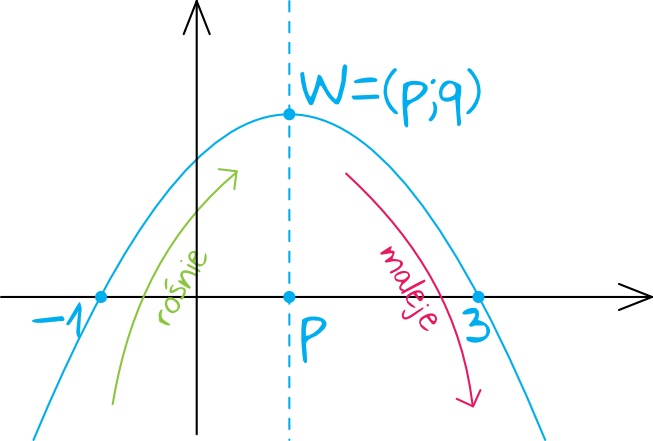
Kluczem do sukcesu jest dostrzeżenie, że funkcja maleje od wierzchołka aż do nieskończoności, zatem musimy poznać współrzędną \(p\) wierzchołka paraboli.
Krok 3. Wyznaczenie współrzędnej \(p\) wierzchołka paraboli.
Z własności parabol wynika, że współrzędna \(p\) jest średnią arytmetyczną miejsc zerowych funkcji kwadratowej (ponieważ wierzchołek znajduje się w jednakowej odległości od obydwu miejsc przecięcia się paraboli z osią \(OX\)). Skoro tak, to:
$$p=\frac{-1+3}{2} \\
p=\frac{2}{2} \\
p=1$$
Krok 4. Ustalenie przedziału, w którym funkcja jest rosnąca.
Zgodnie z tym co sobie powiedzieliśmy, skoro \(p=1\), to funkcja maleje w przedziale \(\langle1,+\infty)\).