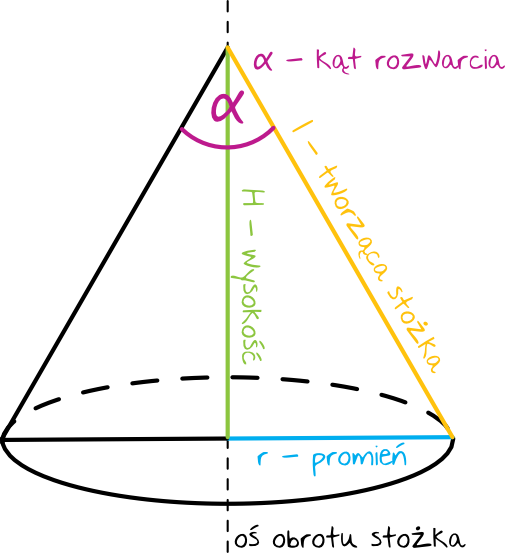
Stożek to bryła obrotowa, która powstaje w wyniku obrotu trójkąta. Stożek w przeciwieństwie do walca ma tylko jedną podstawę w kształcie koła. Kluczowymi miarami w stożku są promień podstawy, wysokość stożka, tworząca stożka oraz kąt rozwarcia.
Rodzaje stożków
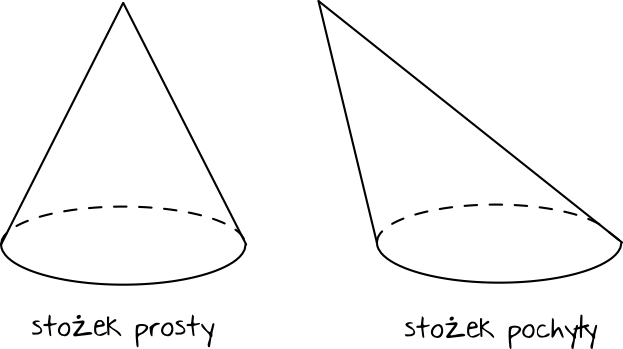
Na matematyce (zwłaszcza na poziomie podstawowym) spotykać się będziemy przede wszystkim ze stożkami prostymi (zwanymi także prawidłowymi). Charakterystyczną cechą stożka prostego jest to, że jego wysokość będzie padać zawsze na środek podstawy. Domyślnie możemy przyjąć, że mówiąc „stożek” mamy na myśli stożek prosty. Warto jednak mieć na uwadze, że stożki w szczególnych przypadkach mogą być także pochyłe.
Oś obrotu stożka
Oś obrotu stożka to prosta wokół której obracany był dany trójkąt. Stożek powstaje najczęściej w wyniku obrotu trójkąta równoramiennego wzdłuż jego osi symetrii lub w wyniku obrotu trójkąta prostokątnego wzdłuż jednej lub drugiej przyprostokątnej:
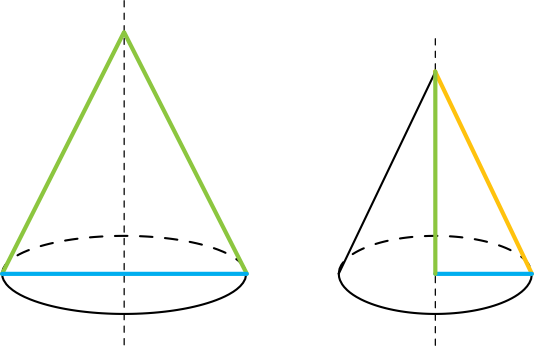
To co dla nas jest ważne to fakt, że oś obrotu stożka prostego zawsze przechodzi przez środek koła znajdującego się w podstawie.
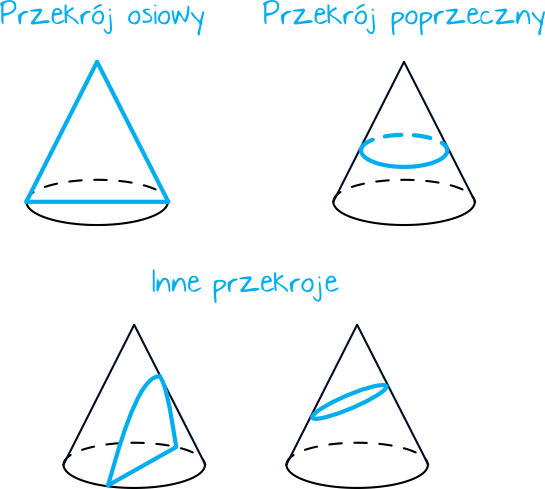
Przekrój stożka
• W przekroju osiowym stożka znajduje się trójkąt. Ważną cechą tego trójkąta jest to, że ten trójkąt jest zawsze równoramienny (o ile oczywiście nie mamy stożka pochyłego).
• W przekroju poprzecznym stożka znajduje się koło.
Siatka stożka
Siatkę walca możemy narysować w ten oto sposób:
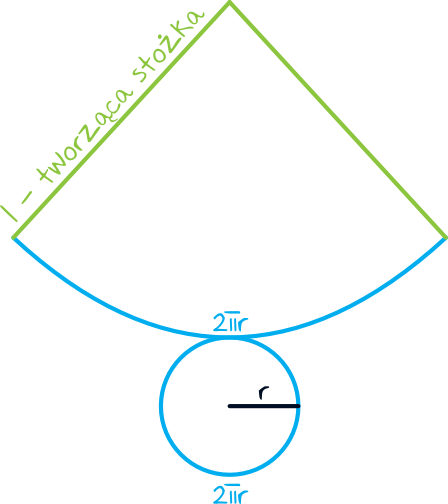
Rysując siatkę stożka należy zwrócić uwagę na to, żeby dolny łuk miał długość \(2πr\), czyli długość obwodu koła znajdującego się w podstawie.
Stożek – wzory
Kluczowymi wzorami związanymi ze stożkiem są:
• Objętość stożka: \(V=\frac{1}{3}πr^2\cdot H\)
• Pole powierzchni całkowitej stożka: \(P_{c}=πr^2+πrl\)
• Pole powierzchni bocznej stożka: \(P_{b}=πrl\)
gdzie:
\(r\) – promień podstawy stożka
\(H\) – wysokość stożka
\(l\) – tworząca stożka
Wszystkie powyższe wzory zostały szerzej omówione (wraz z przykładami) w poniższych tematach:
